Oomph!
- 55
- 0
Hello. I solve this problem:
1. Homework Statement
The particles of mass m moves without friction on the inner wall of the axially symmetric vessel with the equation of the rotational paraboloid:
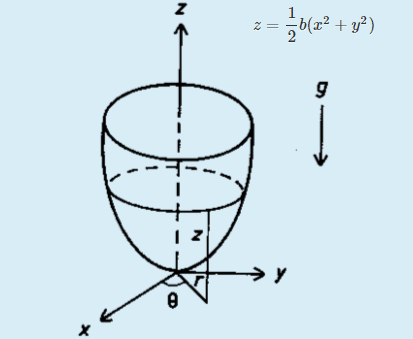
where b>0.
a) The particle moves along the circular trajectory at a height of z = z(0).
express:
- Lagrangian
- the equation of motion for the polar coordinate r
- energy of the particle (with m, z(0), b and g only)
- angular momentum of the particle (with m, z(0), b and g only)
b) We slightly deflect the particles downwards. Find the frequency of small oscillations around the original intact trajectory.
2. Relevant equation
Lagrangian equations, equations for energy in conservative field and angular momentum.
a) I didn't have any problem with Lagrangian and equation of motion for the polar coordinate r. Here is the result, I know how to do it:
- Lagrangian:
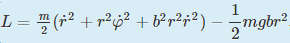 (1)
(1)
- equation of motion for the polar coordinate r:
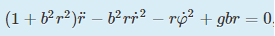 (2)
(2)
I have problem to express the energy and angular momentrum od particle. I show you my attempt:
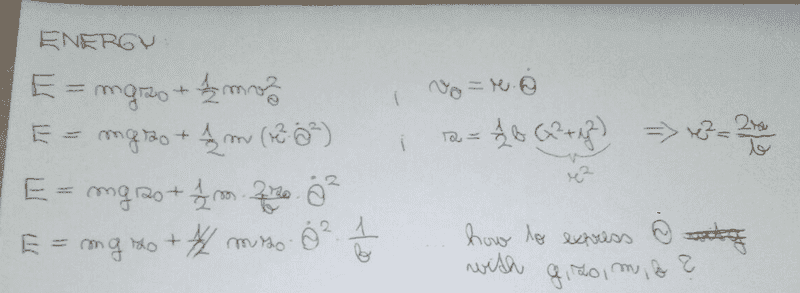
So, the problem is that I don't know, how to express the time derivation of Θ.
Could I just say, that the time derivation of Θ is the (gb)^(1/2) because the equation (2) is in standart form where ω^2=gb?
b) Well, I don't have any idea. I just have the result:
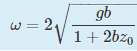
And it doesn't make sense if I told that ω^2=gb.
So, please, could you tell me what is wrong and what to do?
Thank you.
1. Homework Statement
The particles of mass m moves without friction on the inner wall of the axially symmetric vessel with the equation of the rotational paraboloid:
where b>0.
a) The particle moves along the circular trajectory at a height of z = z(0).
express:
- Lagrangian
- the equation of motion for the polar coordinate r
- energy of the particle (with m, z(0), b and g only)
- angular momentum of the particle (with m, z(0), b and g only)
b) We slightly deflect the particles downwards. Find the frequency of small oscillations around the original intact trajectory.
2. Relevant equation
Lagrangian equations, equations for energy in conservative field and angular momentum.
The Attempt at a Solution
a) I didn't have any problem with Lagrangian and equation of motion for the polar coordinate r. Here is the result, I know how to do it:
- Lagrangian:
- equation of motion for the polar coordinate r:
I have problem to express the energy and angular momentrum od particle. I show you my attempt:
So, the problem is that I don't know, how to express the time derivation of Θ.
Could I just say, that the time derivation of Θ is the (gb)^(1/2) because the equation (2) is in standart form where ω^2=gb?
b) Well, I don't have any idea. I just have the result:
And it doesn't make sense if I told that ω^2=gb.
So, please, could you tell me what is wrong and what to do?
Thank you.