Homework Help Overview
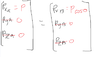
The discussion revolves around a lambda particle decaying into a pion and a proton, with the lambda initially moving at a velocity of 0.9c. Participants are exploring the momentum of the decay products and the implications of conservation laws in this context.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants discuss the ambiguity of having two solutions for momentum and question the physical significance of each. There is a focus on understanding the decay in both the moving and rest frames of the lambda particle. Some participants suggest performing calculations in the lambda's rest frame to clarify the situation.
Discussion Status
The discussion is active, with participants providing guidance on how to approach the problem, particularly regarding the interpretation of momentum in different frames. There is an acknowledgment of the complexity of the decay process and the potential for multiple outcomes based on the decay angle.
Contextual Notes
Participants note the challenge of understanding the implications of momentum conservation and the nature of decay products in a relativistic context. There is mention of the need to consider isotropic decay and the concept of beaming in the analysis.