Laplace Transform Finding Open-Circuit Voltage

[willDavidson]

TL;DR

I am trying to determine how to represent open circuit voltage during laplace transform

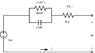
I am interested in modeling a battery charging/discharging. I am starting off with a simple model using a voltage source in series with a parallel RC branch which is in series with a resistor. I will be measuring the open circuit voltage between the last series resistor and the bottom of the source. In the past when I've done Laplace, it was never looking at open circuit voltage but voltage across an element. For this, I'm wondering if I represent the open circuit voltage as a simple voltage source when doing the Laplace transform or is it something more?

 

[willDavidson]

I should've posted a sample of the circuit schematic. I've attached it here.

 

[eq1]

The Laplace transform of a constant, say c, is c/s.

But I think really the answer to your question depends on what the model is for. i.e. If you're looking to model the transient response of a system upon battery insert (or removal) I would just use the standard technique of modeling the source as a step function and put your impedance model in series with that source.

 

[Jody]

I don't think the impedance would matter since it's just an open circuit? There's no current. If I got that question on an exam I would likely say the transform is whatever the source is.

 

[eq1]

I am interested in modeling a battery charging/discharging. ... For this, I'm wondering if I represent the open circuit voltage as a simple voltage source when doing the Laplace transform or is it something more?

I should've read your question more closely. Because of your description of the independent voltage source and the resistor, etc. I assumed your were looking for the small signal response of the battery so you could asses the stability (or general response) of a circuit while charging, or something, at a given operating point.

If you're just looking to model the charge and discharge curve (i.e. charge stored vs open circuit voltage) then I am not sure Laplace is the right mathematical tool for that. I'm confident one could jury rig a model to make it fit but I think it would be pretty unwieldy. I could be wrong though.

If it was limited to a certain range then it could be linear enough where perhaps you could just model it as a capacitor with an initial condition, and that would work well with Laplace. But over the entire operating range batteries are fairly non-linear which makes me think you're probably going to be best off with a time domain model. It still boils down to what question you're asking of the model and what accuracy you require, as always.

See this link for more information on battery charge curves.

https://www.richtek.com/Design Support/Technical Document/AN024

 

[eq1]

This link gives a pretty decent time based circuit model.
https://www.mdpi.com/2313-0105/5/1/31