Laws of Motion (Pulleys, blocks)

[kishlaysingh04]

Homework Statement

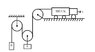
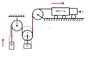
A truck shown in the figure is driven with an acceleration a =3m/s2. Find the acceleration of the
bodies A and B of masses 10 kg and 5 kg respectively, assuming pulleys are mass less and friction is absent everywhere.

The Attempt at a Solution

I have written three equations i.e.

for B: 5a1= T-5g

for A: I don't what to write whether 10a2= 2T-10g or 10a2= 10g-2T

and 2(a1 - a)= a2

I have solved the equations and i have got a1=a2=2m/s2

but the ans is a1=a2=1m/s2

 

[Nathanael]

for A: I don't what to write whether 10a2= 2T-10g or 10a2= 10g-2T

Well it's arbitrary, but it has to be consistent with your first equation. So since you considered the direction of gravity to be negative in your first equation, you must do the same in this equation. So you would use 10a_2=2T-10g


Now about the problem;
Your first two equations combine to give the constraint a_1=a_2 That is half the battle.
Now you just need to find a relationship between a_1 and a_2 (which will likely also relate to the known acceleration of the truck, a)



Your math claims that this relationship is:

2(a_1 - a)= a_2

Can you explain how you came up with this equation?

 

[kishlaysingh04]

oh sorry i have got that wrong, actually I think it should be
a1 - a = 2a2
is this correct?

 

[Nathanael]

Let me ask you, after some time, does the length of the entire rope get shorter? (Or longer?)


P.S.
It can be difficult to help if you don't (at least slightly) explain your math. Why did that equation come to mind?

 

[rbn251]

Hi,
I have also been trying to solve this problem, using the string length method:

If the weight on the left moves up by x, then the string segment on the left decreases by x.
If the weight on the right moves up by y, then the string segment in the middle decreases by y and the string segment on the right decreases by y.

The sum of the differences must be zero so x + 2y = 0.

Then I not sure what to do as this relation just gives a1 = -2a2 ?

Thanks

 

[Nathanael]

If the weight on the right moves up by y, then the string segment in the middle decreases by y and the string segment on the right decreases by y.

If the weight on the right (A) moves up by a distance y, then the string is shortened by a distance 2y, right?

The sum of the differences must be zero so x + 2y = 0.

The sum of how much the rope is shortened must equal the distance that the truck moved to the right.

 

[Vibhor]

but the ans is a1=a2=1m/s2

Are you sure this is the answer given ?

I am getting a_B =19/3ms^-2 downwards and a_A = 14/3 ms^-2 upwards .

 

[Orodruin]

Are you sure this is the answer given ?

I am getting a_B =19/3ms^-2 downwards and a_A = 14/3 ms^-2 upwards .

That the accelerations are the same is relatively straightforward to arrive at. Consider the string tension and the free body diagrams for B and for A+pulley.

 

[Vibhor]

That the accelerations are the same is relatively straightforward to arrive at.Consider the string tension and the free body diagrams for B and for A+pulley.

I don't think we need to consider the forces to determine the relationship between the accelerations of the two blocks .

Could you explain just one thing and that is - how are the accelerations of the two blocks equal ?

May be I am missing something very obvious.

 

[ehild]

Assume both blocks move upward.

a1 is the acceleration of A, a2 is the acceleration of B. The tension in the rope is T.

2T-10g=10a1 divided by 2: T-5g=5a1.
T-5g=5a2. You see that a1=a2.

ehild

 

[Orodruin]

We are given that the mass of B, let us call it $m_B$ is half of the mass of A $m_A = 2 m_B$. If we call the string tension $T$, then the free body diagram for B gives (positive direction down)
$$
m_B g - T = m_B a_B
$$
while that for A gives
$$
m_A g - 2T = m_A a_A \quad \Rightarrow \quad 2(m_B g -T) = 2m_B a_A.
$$
Inserting the first equation into the second gives
$$
a_A = a_B.
$$
In order to relate them to the acceleration of the truck you need to further assume that the string does not change its length.

 

[Vibhor]

Sorry .I realize my mistake .

I was wrongly using mass of A = 5kg and that of B = 10kg , when it should have been the other way round .In addition,there was a sign error . I need to be more careful .

I think I managed to confuse myself quite well .

Thanks Orodruin and ehild !

 

[rbn251]

The other part I have worked out as:

If block B rises by x, then the string length at the truck increases by x.
If block A rises by y, then the string length at the truck increases by 2y.
Let the string length at the truck be z, then z=x+2y.

Differentiating this relation twice, and sub in the known truck acceleration gives:
a_B + 2a_A = 3
which with a_B = a_A gives the solution, 1ms^-2

 

[Vibhor]

Assume both blocks move upward.

a1 is the acceleration of A, a2 is the acceleration of B. The tension in the rope is T.

2T-10g=10a1 divided by 2: T-5g=5a1.
T-5g=5a2. You see that a1=a2.

ehild

The problem is solved but still a few things are unclear .

The point where I confuse myself is where acceleration of string pieces is related to the acceleration of the blocks.This is where sign error creeps in.

Suppose ΔL₁ is the change in horizontal rope length from pulley to the truck.ΔL₂ is the change in vertical rope length to the right of movable pulley .ΔL₃ is the change in vertical rope length to the left of movable pulley .ΔL₄ is the change in vertical rope length from fixed pulley to block B .

If I write ΔL₁ = ΔL₂+ΔL₃+ΔL₄ , I get the correct relation 2x_A+x_B = 3 .

But what is the problem in writing it as ΔL₂ +ΔL₃= ΔL₁+ΔL₄ ? This gives incorrect relation 2x_A=x_B + 3 .

Or, may be writing it as ΔL₄ = ΔL₂+ΔL₃+ΔL₁.This gives x_B=2x_A + 3 .

What am I missing ?

 

[rbn251]

You are right, this is confusing. Really you don't want to consider the direction of the rope wrt the diagram, but wrt the truck. So there are only really two directions the rope moves - to the right or to the left.

(Think about 'unwinding' the rope from the pulleys, and consider it as a straight piece of rope, then there is no distinction of vertical or horizontal rope length)

 

[ehild]

What am I missing ?

You have to suppose some direction which is positive. For ΔL1, it is positive if the truck moves to the right. But that makes the total vertical piece of the rope shorten.

If any of the vertical pieces gets longer and the others do not change, the horizontal rope gets shorter. If the horizontal piece gets longer, and only one vertical piece changes length, that piece gets shorter. You can decide about the signs of ΔLi. If you assume they are positive in case the rope gets shorter than you have the equation ΔL2+ΔL3+ΔL4=ΔL1.
In case you consider ΔLi positive if the length increases, you have the equation ΔL1+ΔL2+ΔL3+ΔL4=0. But then you have to reconsider how the ΔL-s are related to the displacements of the blocks.

ehild

 

[Vibhor]

You can decide about the signs of ΔLi. If you assume they are positive in case the rope gets shorter than you have the equation ΔL2+ΔL3+ΔL4=ΔL1.

In this case ΔL4 would be negative as the rope from fixed pulley to block B increases .Isn't it ?

In case you consider ΔLi positive if the length increases, you have the equation ΔL1+ΔL2+ΔL3+ΔL4=0. But then you have to reconsider how the ΔL-s are related to the displacements of the blocks.

Same issue here . I think whatever is assumption ,ΔL2+ΔL3 and ΔL4 would have opposite signs , as when the rope length to block A increases , that to block B decreases and vica versa .

 

[ehild]

No, both blocks rise, and that makes the length of the attached pieces shorten.

ehild

 

[Vibhor]

No, both blocks rise.

How did you conclude that ?

If block A rises,middle rope length shortens ,this is compensated by truck moving to right and block B going down .

What makes you deduce that block B goes up as well ?

 

[ehild]

How did you conclude that ?

We got that a1=a2.

If block A rises,middle rope length shortens ,this is compensated by truck moving to right and block B going down .

Why?

What makes you deduce that block B goes up as well ?

As it came out, a1=a2=1m/s².


ehild

 

[Vibhor]

Sorry . I don't know why I overlooked that result .In that case first part of assumption in post#16 makes sense .

Now to second part .

In case you consider ΔLi positive if the length increases, you have the equation ΔL1+ΔL2+ΔL3+ΔL4=0. But then you have to reconsider how the ΔL-s are related to the displacements of the blocks.

Shouldn't that be ΔL2+ΔL3+ΔL4= ΔL1,the same result we got before ?

But then you have to reconsider how the ΔL-s are related to the displacements of the blocks.

Could you explain this part ?

 

[ehild]

Sorry . I don't know why I overlooked that result .In that case first part of assumption in post#16 makes sense .

Now to second part .
Shouldn't that be ΔL2+ΔL3+ΔL4= ΔL1,the same result we got before ?

From ΔL1+ΔL2+ΔL3+ΔL4=0 ΔL1+ΔL2+ΔL3=-ΔL4 follows. ehild