LC resonance with high Q factor, Inductor with non magnetic core

  • B
  • Thread starter StoyanNikolov
  • Start date
  • Tags
    Inductor
In summary, an LC resonance circuit with a high Q factor indicates that the circuit has low energy loss and can oscillate at a specific resonant frequency for an extended period. An inductor with a non-magnetic core typically exhibits this high Q factor due to reduced eddy currents and hysteresis losses, making it suitable for applications requiring high efficiency and selectivity, such as in radio frequency circuits and filters.
  • #1
StoyanNikolov
50
0
TL;DR Summary
Lc resonance with high Q factor. Inductor with non magnetic core and air gap
Consider Inductor with air gap and solid metal core made from material with relative magnetic permeability 1 regardless of temperature (such as copper or aluminium).
There is Air gap between coil and metal core

IMG-46115e6ae36f891ba72366ded3739868-V.jpg
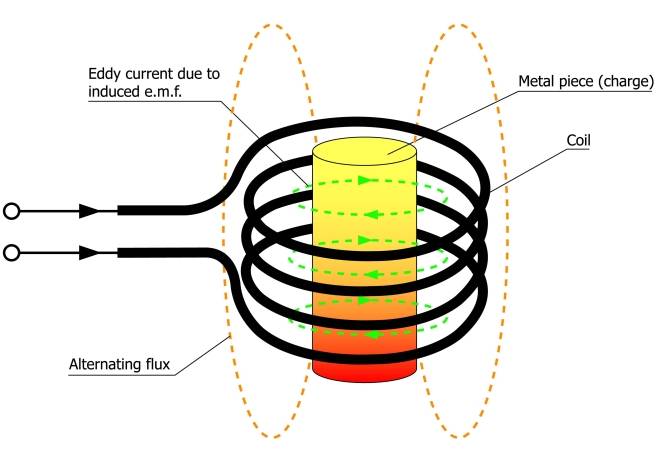Please Also consider Eddy currents in the solid metal core.
The Inductor is connected with capacitor in

Series LC circuit

Parallel LC circuit

Is it possible under certain values of frequency and capacitance to obtain lc resonance with high q factor?
 
Physics news on Phys.org
  • #2
StoyanNikolov said:
TL;DR Summary: Lc resonance with high Q factor. Inductor with non magnetic core and air gap

Is it possible under certain values of frequency and capacitance to obtain lc resonance with high q factor?
No. The eddy current heating of the core will be significant, and so will preclude a high Q. But then your definition of high Q may be different from mine.

An LC tank circuit could be driven to oscillate at its resonant frequency, but the active oscillator element would need to make up the energy lost to the eddy currents in the core.
 
  • #3
Baluncore said:
No. The eddy current heating of the core will be significant, and so will preclude a high Q. But then your definition of high Q may be different from mine.

An LC tank circuit could be driven to oscillate at its resonant frequency, but the active oscillator element would need to make up the energy lost to the eddy currents in the core.
Let's say Is it possible with certain values of Capacitance and Frequency to obtain Resonance with Q above 20 for the given LC Circuit?
 
  • #4
StoyanNikolov said:
Let's say Is it possible with certain values of Capacitance and Frequency to obtain Resonance with Q above 20 for the given LC Circuit?
Why would you say that?
You could design it to have a Q of 20.
What are the dimensions of the coil and the core?
Why is Q relevant?
 
  • #5
Baluncore said:
Why would you say that?
You could design it to have a Q of 20.
What are the dimensions of the coil and the core?
Why is Q relevant?
With current Inductor with Solid Metal Core and the Eddy currents. Is it possible to have Q above 20. Inductor(with solid metal core) , Values of Capacitance of the Capacitor (Switched in Parallel or in Series) and input Frequency
 
Last edited:

FAQ: LC resonance with high Q factor, Inductor with non magnetic core

What is an LC resonance with a high Q factor?

LC resonance refers to the condition in a circuit where an inductor (L) and a capacitor (C) oscillate at their natural resonant frequency. A high Q factor, or quality factor, indicates that the circuit has low energy losses relative to the energy stored in the resonant components, resulting in a sharp and well-defined resonance peak.

Why use an inductor with a non-magnetic core in an LC resonant circuit?

An inductor with a non-magnetic core is often used in LC resonant circuits to minimize core losses and non-linearities. Non-magnetic cores, such as air cores, do not exhibit hysteresis and eddy current losses, which can degrade the performance of the resonant circuit and lower its Q factor.

How does the Q factor affect the performance of an LC resonant circuit?

The Q factor affects the selectivity and bandwidth of an LC resonant circuit. A higher Q factor means the circuit has a narrow bandwidth and high selectivity, making it capable of distinguishing between closely spaced frequencies. This is particularly important in applications like filters and oscillators.

What are the typical applications of high Q LC resonant circuits with non-magnetic core inductors?

High Q LC resonant circuits with non-magnetic core inductors are commonly used in radio frequency (RF) applications, including filters, oscillators, and tuners. They are also used in precision measurement equipment and in applications where minimal signal loss and high frequency stability are required.

How can the Q factor of an LC resonant circuit be maximized?

The Q factor can be maximized by using components with low intrinsic losses. For inductors, this means using non-magnetic cores to avoid core losses and selecting wire with low resistance. For capacitors, choosing high-quality, low-loss dielectric materials is essential. Additionally, minimizing parasitic resistances and ensuring good circuit design practices can help maximize the Q factor.

Similar threads

B Inductive Reactance of Solenoid with Solid Metal Core With respect to frquency
Replies
5
Views
1K
Induction heater with high Q factor
Replies
8
Views
1K
Formula for Resonant Frequency of 2 Metal Coaxial Cylinders?
Replies
10
Views
1K
B Why does my LC circuit not oscillate its energy between Electric & Magnetic fields?
5
Replies
152
Views
3K
H-field and MMF in a magnetic circuit
Replies
25
Views
3K
Why does my inductor coil have no effect on my circuit
Replies
8
Views
2K
Need help, Series RLC resonance circuit, not getting high voltage
Replies
4
Views
2K
B Ion Trap and Time-Varying Potentials
Replies
1
Views
1K
Calculating Q-Factor and Resistance for Series LC Filters
Replies
4
Views
1K
How to know when an LC circuit hits resonance
Replies
32
Views
4K

Hot Threads

Recent Insights

Back
Top