Lebesgue Integration of Simple Functions .... Lindstrom, Lemma 7.4.6 ...

[Math Amateur]

TL;DR

I need help in order to fully understand Lindstrom's proof of Lemma 7.4.6 concerning the Lebesgue integration of an increasing sequence of simple functions ...

I am reading Tom L. Lindstrom's book: Spaces: An Introduction to Real Analysis ... and I am focused on Chapter 7: Measure and Integration ...

I need help with the proof of Lemma 7.4.6 ...

Lemma 7.4.6 and its proof read as follows:

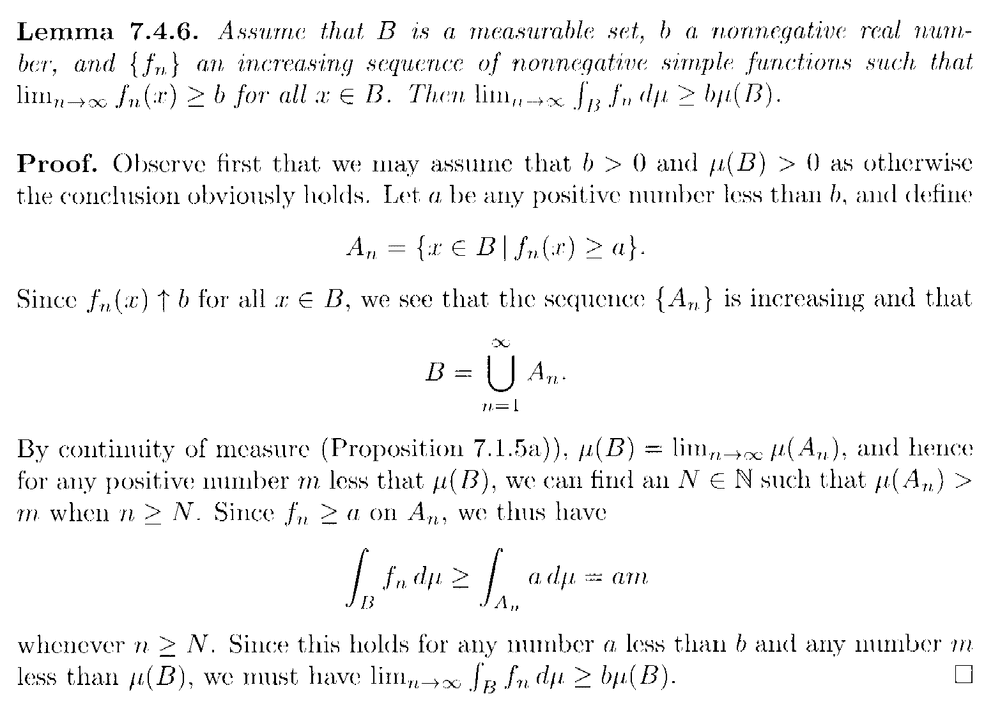
In the above proof by Lindstrom we read the following:

" ... ... Since this holds for any number $a$ less than $b$ and any number $m$ less than $\mu (B)$, we must have $\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$. ... ... "I need help in order to show, formally and rigorously, that $\lim_{ n \to \infty } \int_B f_n d \mu \geq b \mu (B)$ ... ...My thoughts are that we could assume that $\lim_{ n \to \infty } \int_B f_n d \mu \lt b \mu (B)$ ... ... and proceed to demonstrate a contradiction ... but I'm not sure how to formally proceed ... ...

Help will be much appreciated ...

Peter

=================================================================================================================


Readers of the above post may be assisted by access to Lindstrom's introduction to the integration of simple functions ... so I am providing access to the relevant text ... as follows:

Hope that helps ...

Peter

 

[member 587159]

Note that $L:= \lim_n \int_B f_n d \mu$ always exists (possibly with value $\infty$), because it is the limit of an increasing sequence.

The claim the proof makes is:

$$\forall m < \mu(B), \forall a < b : am \leq L \implies b\mu(B) \leq L$$

Fix $a < b$, taking the limit $m \to \mu(B)-$ (limit from the left) of $am \leq L$, we obtain $a \mu(B) \leq L$. Since this holds for all $a < b$, you can take the limit $a \to b-$ (again limit from the left) to obtain $b \mu(B) \leq L$.

Basically, this boils down to showing that limits preserve (non-strict) inequalities of functions, which you probably already know since you are studying measure theory.

 

[andrewkirk]

The answer lies in our total freedom to choose both $a\in(0,b)$ and $m\in(0,\mu(B))$. Let $a=b-h$ and $m=\mu(B)-h$ where we can choose any $h$ such that $0<h<\min(b,\mu(B))$.
Then

\begin{align*}
\lim_{n\to\infty} \int_B f_n\ d\mu
&\ge \lim_{n\to\infty} am
=am
= (b-h)(\mu(B)-h)
= (b\mu(B)-h\mu(B) -bh +h^2)\\
& =b\mu(B)-h\mu(B) -bh +h^2
> b\mu(B)-h(\mu(B)+b)
\end{align*}

whence
\begin{equation*}
\lim_{n\to\infty} \int_B f_n\ d\mu > b\mu(B)-h(\mu(B)+b)\ \ \ \textrm{(A)}
\end{equation*}
Now suppose the contrary of the theorem's result, that $\lim_{n\to\infty} \int_B f_n\ d\mu = b\mu(B)-k$ for some $k>0$.

Then choose $h= \min\left(b/2,\mu(B)/2, \frac k{2(\mu(B)+b)}\right)$, which we noted above that we are free to do. Substitute that expression for $h$ into RHS of (A) and you will get a contradiction:
$$\lim_{n\to\infty} \int_B f_n\ d\mu > b\mu(B)-k/2
> b\mu(B)-k = \lim_{n\to\infty} \int_B f_n\ d\mu$$

 

[Math Amateur]

Thanks to Andrew and Math_QED for most helpful posts ...

Working carefully through your proofs now ...

BUT ... I have another question ...

In the above proof by Lindstrom we read the following:

" ... ... Since $f_n (x) \uparrow b$ for all $x \in B$ ... ... "Unless I am misunderstanding the notation, $f_n (x) \uparrow b$ means $f_n$ tends to $b$ from below ... but ... all we are given is that $\lim_{n \to \infty } f_n (x) \geq b$ which surely is not the same ...

Can someone please clarify this issue ...

Peter

 

[member 587159]

Thanks to Andrew and Math_QED for most helpful posts ...

Working carefully through your proofs now ...

BUT ... I have another question ...

In the above proof by Lindstrom we read the following:

" ... ... Since $f_n (x) \uparrow b$ for all $x \in B$ ... ... "Unless I am misunderstanding the notation, $f_n (x) \uparrow b$ means $f_n$ tends to $b$ from below ... but ... all we are given is that $\lim_{n \to \infty } f_n (x) \geq b$ which surely is not the same ...

Can someone please clarify this issue ...

Peter

That notation means that the sequence is non-decreasing, which is a hypothesis.

 

[Math Amateur]

Oh ... OK ... thanks ...

Peter

 

[andrewkirk]

In the above proof by Lindstrom we read the following:

" ... ... Since $f_n (x) \uparrow b$ for all $x \in B$ ... ... "Unless I am misunderstanding the notation, $f_n (x) \uparrow b$ means $f_n$ tends to $b$ from below

It is justified by the theorem stating that $\{f_n\}$ is an "increasing sequence of non-negative simple functions." By "increasing", it means that $\forall x:\ \forall n:\ f_{n+1}(x) > f_n(x)$.