jack476
- 327
- 124
For a circle with radius R centered at R along the X-axis so that the edge of the circle touches the origin, what is the length of a line drawn between the origin and an edge of the circle in terms of the angle between that line and the X-axis? This isn't a homework problem, just something I'm trying to figure out.
IE in this picture (sorry about the MS Paint, I'm on a fairly old computer right now), what is the length of the line L in terms of the angle a and radius R? Any help is much appreciated, thank you.
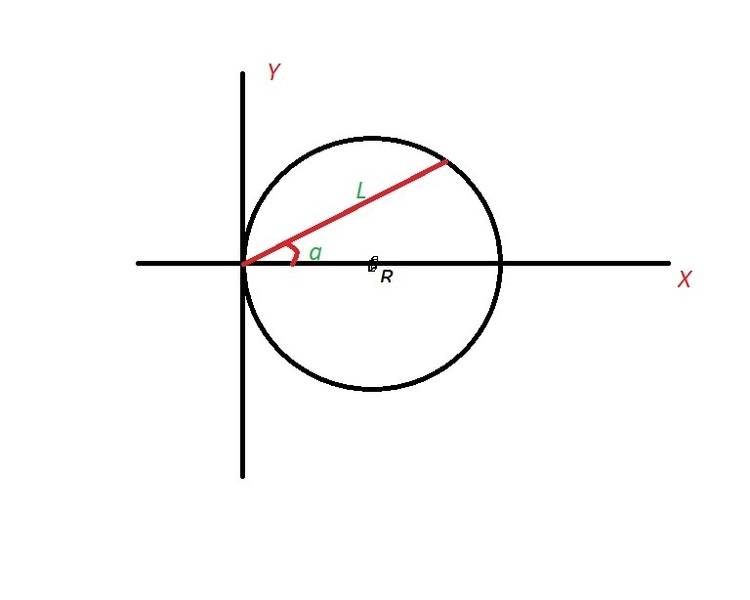
IE in this picture (sorry about the MS Paint, I'm on a fairly old computer right now), what is the length of the line L in terms of the angle a and radius R? Any help is much appreciated, thank you.