Length of a Wave Train in Special Relativity

[Mark Zhu]

Homework Statement

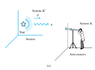
Consider a source of light (for example, a star) and a receiver (an astronomer) approaching one another with a relative velocity v. First we consider the
receiver fixed (Figure 2.27a) in system K and the light source in system K moving toward the receiver with velocity v. The source emits n waves during the time
interval T. Because the speed of light is always c and the source is moving with
velocity v, the total distance between the front and rear of the wave train emitted
during the time interval T is

Relevant Equations

Length of wave train = cT - vT

I am confused about how to find the length of a wave train emitted within a time interval T and that is moving with speed c relative to a moving frame that is itself moving with velocity v. Apparently the answer is that the wave train's length is cT - vT, but I tried to plug in variables into the Lorentz velocity transformation equation in the x direction and didn't get the right answer. I also tried to use the time dilation and length contraction equations but to no avail. Please see attachment for the figure.
Also, I am unsure whether the textbook is trying to find the proper length or is trying to find the length with respect to the stationary frame.

 

[PeroK]

In frame K:

1) What is the definition of the length of the wave train?

2) Where is the first wave when the last wave is emitted.

3) Where is the source when the last wave is emitted.

Bonus question:

4) What do time dilation, length contraction and the Lorentz Transformation have to do with measurements made in frame K?

 

[Mark Zhu]

1) It is the length of the wave as seen by the astronomer.
2) v/(1-v^2/c^2)
3) v/(1-v^2/c^2)
4) Because the frame K' is moving at a constant velocity with respect to frame K at an unknown velocity v, we want to use relativity.

So you're saying we don't need to view it in relativistic terms? I thought that a star would move at a speed >= 0.5c.

 

[PeroK]

Your answers to 2) and 3) are velocities. The question asked for positions.

The Lorentz Transformation relates spacetime coordinates between two inertial reference frames. In this case all the data is given in one frame, so you don't need to transform anything.

The value of $v$ is not relevant to how you solve a kinematic problem.

 

[Mark Zhu]

Ok, that is confusing because I was told to use Lorentz Transformation when dealing with speeds near the speed of light, and in this case the light is traveling at speed c.

 

[PeroK]

Ok, that is confusing because I was told to use Lorentz Transformation when dealing with speeds near the speed of light, and in this case the light is traveling at speed c.

If you were in the lab and had a light source and a detector 10m apart, how long would it take the light to travel from the source to the detector - as measured in the lab frame?

 

[Mark Zhu]

3.3 x 10^-8 s. When it comes to time, however, the textbook relates the proper time to the time as seen by the astronomer in frame K.

 

[PeroK]

3.3 x 10^-8 s.

You didn't use the Lorentz Transformation?

When it comes to time, however, the textbook relates the proper time to the time as seen by the astronomer in frame K.

I can't make any sense of that. What proper time?

The source emits n waves during the time
interval T.

I assume that's time $T$ in the astronomer's frame.

 

[Mark Zhu]

I understand now, thanks.
Btw, I meant when the textbook calculates the frequency of the wave in frame K, it uses Lorentz transformations.

 

[etotheipi]

You must either be misunderstanding something or otherwise the book must be wrong, since the Lorentz transformations are a coordinate transformation between two inertial frames. To answer @PeroK's bonus question: nada.

The first wave emitted by the source travels $cT$ during the interval $T$, and the source travels $vT$. The distance between the front wave and the source is $cT-vT$. The resulting wavelength in $K$ is this distance divided into $n$ pieces, i.e. $\lambda = \frac{cT - vT}{n}$.

 

[PeroK]

I understand now, thanks.
Btw, I meant when the textbook calculates the frequency of the wave in frame K, it uses Lorentz transformations.

The question ought to give the frequency in the frame of the source: $n$ waves in $T'$ seconds. Then, you would need to use time dilation and the question would have some requirement for SR.

But, the answer is just the simple kinematic answer. So, clearly, they intended $T$to be the time in the astronomer's frame and it's just a simple kinematic problem.

I was going to say that it's almost a trick question. Maybe it is a trick question. On the other hand, you can't go applying the Lorentz Transformation willy-nilly!

 

[Mark Zhu]

Actually, it does later say,
"In its rest frame, the source emits n waves of frequency f0 during the proper time T0'. n = f0T0'."

 

[PeroK]

Actually, it does later say,
"In its rest frame, the source emits n waves of frequency f0 during the proper time T0'. n = f0T0'."

Yes, but first it gives you $T$ in the astronomer's frame.

You ought to have recognised that $cT - vT$ is simply the distance that opens up between light traveling at $c$ and a source traveling at $v$ in $T$ seconds. See post #10.

 

[etotheipi]

@PeroK's suggestion in #11 is very good. In the rest frame of the source let's say the time interval between the first and last emissions is $T'$. Because the emissions occur at the same spatial location in the source frame $K'$, we can use the time dilation formula $T = \gamma T'$. Notice that$$\lambda = \frac{(c-v)T}{n} = \frac{(c-v)\gamma T'}{n}$$ Since $n = fT = f'T'$ (i.e. the number of wavefronts is frame invariant),$$f = \frac{c}{\lambda} = \frac{cn}{(c-v)\gamma T'} \frac{c^{-1}}{c^{-1}} = \frac{f' T'}{(1-\frac{v}{c}) \gamma T'} = \frac{\sqrt{1-\frac{v^2}{c^2}}}{1-\frac{v}{c}} f' = \frac{\sqrt{1+\frac{v}{c}}}{\sqrt{1-\frac{v}{c}}} f' = \frac{\sqrt{1+\beta}}{\sqrt{1-\beta}} f'$$This equation should be familiar, it's the Doppler effect!

______________________
N.B. out of interest, there is a more direct way to obtain this relation; consider another completely different scenario where we have two frames $S$ and $S'$. A two-dimensional wave in $S$ is described (up to a constant phase shift) by $y = f(kx - \omega t)$, where $f$ could be, for instance, a $\sin$ function, and $\omega = ck$.

Let $S'$ move at $\beta_x$ w.r.t $S$, then the Lorentz transformation spits out $x = \gamma (x'+c\beta_x t')$ and $t =\gamma(t' + \frac{\beta_x x'}{c})$. Plug these into the equation of the wave, keeping in mind that here $y=y'$, $$\begin{align*}y' = f\left( k(\gamma (x'+c\beta_x t')) -\omega (\gamma(t' + \frac{x'\beta_x}{c}) \right) &=f\left( (k\gamma - \frac{\omega \gamma \beta_x}{c}) x' - (\omega \gamma - k\gamma c\beta_x) t' \right)\\&= f\left(
(1 - \beta_x) k \gamma x' - (1-\beta_x) \omega \gamma t'
\right)\end{align*}$$Then you can identify $\omega' = (1-\beta_x) \gamma \omega = \frac{\sqrt{1-\beta_x}}{\sqrt{1+\beta_x}} \omega$ which you can invert to find$$\omega' = \frac{\sqrt{1+\beta_x}}{\sqrt{1-\beta_x}} \omega$$