- #1
Genilson
- 6
- 0
Hello good evening to all, I was studying here and got stuck with this.
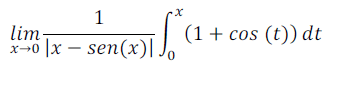
I solved the integral and got [x+sin(x) -1]
and that´s the farthest that I got. I would appreciate the help.
I solved the integral and got [x+sin(x) -1]
and that´s the farthest that I got. I would appreciate the help.