Linear Algebra / Linear Maps (Transformations)

[Hypercube]

This isn't really a homework question, I just need help understanding the example:

=====================

====================

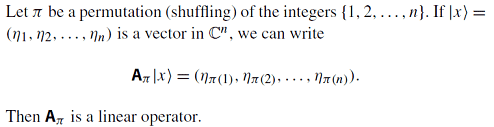
So transformation takes complex n-tuple as input, and it seems output is also a complex n-tuple (which is what makes it "operator"). But permutations of n entries is not n. I'm confused! Let's use the simple example, let x = (1, 2, 3). Permutations of this vector would be a set of 3! entries:

{(1, 2, 3),(1, 3, 2),(2, 1, 3),(2, 3, 1),(3, 1, 2),(3, 2, 1)}

But the transformation seems to produce one single ordered n-tuple, rather than a whole set.

Alternative interpretation would be that entries in the range of T: eta₁, eta₂, eta₃, ..., eta_n are the number of permutations of the first n elements. But that also makes no sense, I would end up with a sequence of natural numbers that do not depend on the input vector.

I must be misunderstanding something, and I have a feeling it's obvious. Any help would be appreciated, thanks in advance.

(Note to moderator: I have not used the template since it is not applicable; no questions nor relevant equations. My thoughts and effort on the example have been included though. Also, apologies if I am posting in the wrong place.)

 

[FactChecker]

So transformation takes complex n-tuple as input, and it seems output is also a complex n-tuple (which is what makes it "operator"). But permutations of n entries is not n. I'm confused! Let's use the simple example, let x = (1, 2, 3). Permutations of this vector would be a set of 3! entries:

That is not relevant to this problem. We are just talking about one particular permutation, π, not how many different ones there might be. A_π is just one particular way of shuffling the elements of x.

 

[Hypercube]

That is not relevant to this problem. We are just talking about one particular permutation, π, not how many different ones there might be. A_π is just one particular way of shuffling the elements of x.

You are right! I was just about to post that I have figured it out. Thank you for your reply!