Linear and angular momentum problem

[barryj]

This is not a homework problem.
I am trying to set up the following problem. I am doing something wrong. Help. I have attached the problem and figure but here is the text.

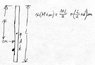
Figure 10-52 shows a thin, uniform bar of Length L and mass M and a small blob of putty of mass m. The system is supported by a frictionless horizontal surface. The putty moves to the right with a velocity v, strikes the bar at a distance d from the center of the bar, and sticks to the bar at the point of contact. Obtain expression for the velocity of the system's center of mass and for the angular speed following the collision.

To find the angular speed, I use the conservation of angular momentum.

mv(1)d = m*v(2)*d + (1/12)ML^2 * V(2)

Is this a correct setup?

Thanks
Barry

 

[Doc Al]

Compute the angular momentum about the center of mass of the system.

 

[barryj]

Thanks Doc Al, I think I see your point. When the putty hits the bar, the rotation is about the center of mass of the rod/putty combination and will be between the center of the rod and the putty as I how on my attachment. Yes?

 

[Doc Al]

Thanks Doc Al, I think I see your point. When the putty hits the bar, the rotation is about the center of mass of the rod/putty combination and will be between the center of the rod and the putty as I how on my attachment. Yes?

Yes, that's correct. Now figure out the speed of the bullet and the bar in the center of mass frame.

 

[Nickie]

Hello Barry,

Thank you for sharing your problem and question. It seems like you are on the right track in setting up your problem and using the conservation of angular momentum to find the angular speed. However, there are a few things that can be improved in your setup.

Firstly, when using the conservation of angular momentum, it is important to define a reference point or axis around which the angular momentum is conserved. In this case, since the system is supported by a frictionless horizontal surface, it would be best to choose the point of contact between the bar and the surface as the reference point. This means that the angular momentum before and after the collision should be calculated with respect to this point.

Secondly, the equation you have written for the conservation of angular momentum is not entirely correct. The correct equation should be:

m*v(1)*d = (m+M)*v(2)*d + (1/12)ML^2 * w(2)

where w(2) is the angular speed of the system after the collision. This equation takes into account the fact that the putty sticks to the bar and becomes part of the system, increasing its mass.

Lastly, it is important to note that the velocity of the center of mass of the system will remain the same before and after the collision, as there are no external forces acting on the system. Therefore, the equation for the conservation of linear momentum can also be used to solve for the velocity of the center of mass.

I hope this helps. Good luck with your problem!