Luna Lunaticus
1. Problem
Recall that we defined linear equations as those whose solutions can be superposed to find more solutions. Which of the following differential/integral equations are linear equations for the function u(x,t)? Below, a and b are constants, c is the speed of light, and f(x,t) is an arbitrary function of x and t.
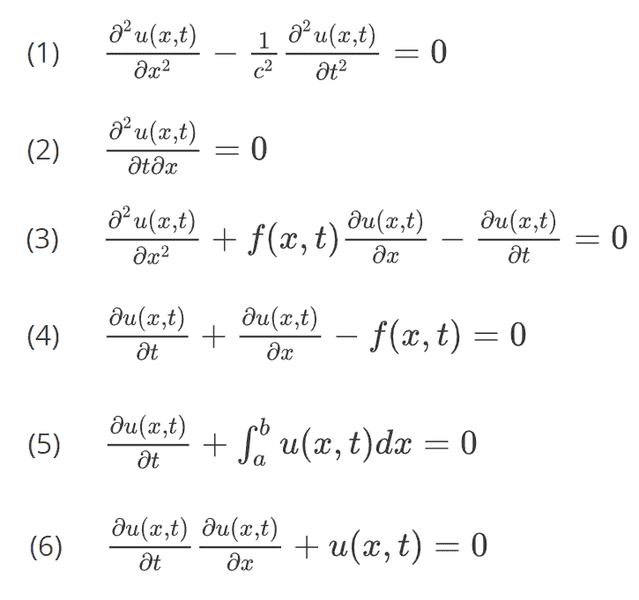
Do not try to solve this excercise using knowledge of "differential equations etc etc etc". APPLY "linearity properties".
You check it by the same way for all the equations: substitute in u(x,t) with G(x,t)+H(x,t) and see if the end result is L(G+H)=L(G) + L(H). Then check by substituting in a*u(x,t) where “a” is a constant to see if you get L(a*u)=a*L(u).If you have L(G+H)=L(G)+L(H) and L(a*u)=a*L(u), then it must be linear.
I'm very slow at calculus, so I was asking for some help to solve this while learning a bit of MathLab.
Recall that we defined linear equations as those whose solutions can be superposed to find more solutions. Which of the following differential/integral equations are linear equations for the function u(x,t)? Below, a and b are constants, c is the speed of light, and f(x,t) is an arbitrary function of x and t.
Homework Equations
Do not try to solve this excercise using knowledge of "differential equations etc etc etc". APPLY "linearity properties".
You check it by the same way for all the equations: substitute in u(x,t) with G(x,t)+H(x,t) and see if the end result is L(G+H)=L(G) + L(H). Then check by substituting in a*u(x,t) where “a” is a constant to see if you get L(a*u)=a*L(u).If you have L(G+H)=L(G)+L(H) and L(a*u)=a*L(u), then it must be linear.
The Attempt at a Solution
I'm very slow at calculus, so I was asking for some help to solve this while learning a bit of MathLab.