Liquid temperature increases when flowing through a 100% efficient pump?

[oksuz_]

Hi,

For an ideal Rankine cycle,

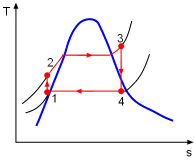
the temperature-specific entropy diagram can be given as follows,

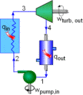
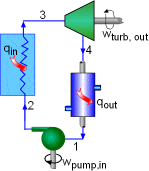
The pump in this cycle is isentropically 100% efficient.

My question is that why the temperature of the water increases as it flows through the pump (point 1 to 2) if the pump is 100% efficient. I can understand why point 2 is not on the saturation line (need higher temperature at a higher pressure to make a liquid saturated).

Thank you in advance.

 

[PeterDonis]

why the temperature of the water increases as it flows through the pump (point 1 to 2) if the pump is 100% efficient.

What does the pump do to the water? It doesn't increase its entropy (since it's 100% efficient), but it has to do something in order to make the water flow. What is that something?

 

[oksuz_]

It exerts a force (pressure) on the water. If the working fluid was gas, the pressure would increase its temperature. However, we are considering an incompressible fluid. Definitely, I am missing something.

 

[russ_watters]

It exerts a force (pressure) on the water. If the working fluid was gas, the pressure would increase its temperature. However, we are considering an incompressible fluid. Definitely, I am missing something.

Your constraints are contradicting each other. You are asking about what happens when water is compressed, while saying you want to consider water to be incompressible. You have to pick one.

I do have an easy way out though: the effect you are asking about is almost nonexistent, so you can just ignore it. It is exaggerated on the generic diagram you posted so it can be seen. Look at a real t-s diagram for water and you'll have trouble even seeing it to quantify it.