Looking for insight into what the Determinant means....

[kostoglotov]

In HS they just taught you the formula for it (the cofactor method) and a few other things, such as det(A) = 0 means A is singular.

I finally reached Ch 5 of MIT OCW Intro to Linear Algebra, and I was really hoping that seeing how determinants are derived from first principles would give me some insight into what the determinant means...aside from whether or not the matrix is singular. I can follow the derivation, through the Big Formula, using the first three properties (det(I) = 1, row swap multiplies by -1, and linearity of determinants).

I have seen how the A \times adj(A) = det(A)\times I

I have shown myself how the determinant for a 2x2 and 3x3 matrix arises purely from elimination, and considering the case if the last pivot is zero.

Ie:

\begin{bmatrix}a & b\\ 0 & d-\frac{bc}{a}\end{bmatrix}

and

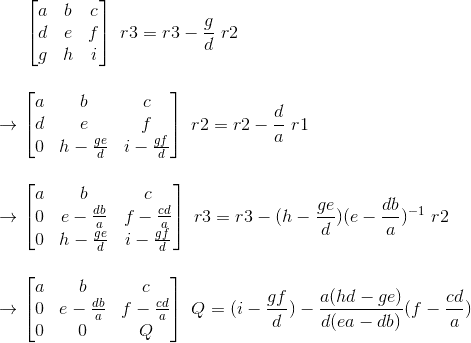
imgur link: http://i.imgur.com/BDjXWcn.gif

What I've learned now just begs a further question, rather than, "why is the determinant important/ what does the determinant means?", I am now wondering, "what do the pivots, and the product of the pivots mean?" Aside of course from indicating whether or not the matrix is singular.

 

[Fredrik]

You would probably like the chapter on determinants in Treil: http://www.math.brown.edu/~treil/papers/LADW/LADW.html

 

[rs1n]

The determinant can be interpreted geometrically. If A is an n\times n matrix, then let r_1, r_2, \dotsm, r_n be the n rows of A. The absolute value of the determinant of A would be the n-dimensional voume of the parallelotope corresponding to these n vectors. (Imagine one corner of the polytope at the origin, and n more corners located at r_i.) If the determinant is non-zero, then A has an inverse. Geometrically, this means there is a bijective map f:\mathbb{R}^n \to \mathbb{R}^n such that f(A) = I. That is, there is a linear transformation (namely f(x)=A^{-1}x) that maps the parallelotope associated with A to the unit parallelotope associated with the identity matrix I. In the case where the determinant (and hence volume) is 0, the parallelotope is degenerate. (In \mathbb{R}^3, one such case would be a box with height 0, so that it is really a flat square inside 3-dimensional space). As your intuition might suggest, any mapping that takes such a degenerate polytope to the unit parallelotope could not possibly be bijective.