Looking for what I thought would be a simple Permeability Q

[tim9000]

Hi, I've been thinking about how to calculate a permeability curve, I thought this would be an easy to find online but unfortunately I haven't had any luck.
From what I can graphically see below:

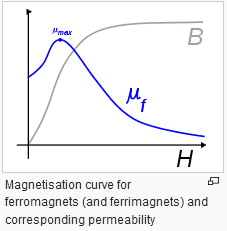
It appears to me that mu for a ferromagnetic material is proportional to the derivative of B vs H, but if this is true, and if so what the actual relation is I haven't been able to find.

Anyone know?

Thanks

 

[Svein]

See http://en.wikipedia.org/wiki/Magnetic_hysteresis

 

[NascentOxygen]

It appears to me that mu for a ferromagnetic material is proportional to the derivative of B vs H

That's an astute observation! The graph does indeed bear that resemblance.

Let's see ...

B and H are related in the usual way, viz., B=μH

Since μ changes with H, we can say μ is a function of H, writing this as μ(H). Accordingly, we can
write the equation more generally as B = μ(H).H

So, dB/dH = H.dμ/dH + μ

Now, on the right side if the first term were small in relation to the second (and you would need to look at typical values and graphs to see where this approximate could apply) you'd have your approximation

μ ≈ dB/dH http://imageshack.com/a/img29/6853/xn4n.gif

 

[tim9000]

See http://en.wikipedia.org/wiki/Magnetic_hysteresis

Hi, I remember what a hysteresis curve is, but I don't see what it has to do with finding the mu of a steel.

That's an astute observation! The graph does indeed bear that resemblance.

Let's see ...

B and H are related in the usual way, viz., B=μH

Since μ changes with H, we can say μ is a function of H, writing this as μ(H). Accordingly, we can
write the equation more generally as B = μ(H).H

So, dB/dH = H.dμ/dH + μ

Now, on the right side if the first term were small in relation to the second (and you would need to look at typical values and graphs to see where this approximate could apply) you'd have your approximation

μ ≈ dB/dH http://imageshack.com/a/img29/6853/xn4n.gif

I'm sorry it's been so long since I've done multivariable calculus, I'm sure that was simple but could you tell me the working, did you use implicit or partial differentiation? Or just the old product or chain rule?

So since μ = dB/dH - H.dμ/dH
to calculate current μ you could just use a previous value of μ in H.dμ/dH, for a really close approximation. What units would dB/dH be in? Because B is in Teslas, I'm assuming it would be in too, as the graph indicates, but I notice it is H/m, does this mean the graph isn't scaled correctly?

Thanks

 

[NascentOxygen]

In that differentiation I used the derivative of a product rule.

dB/dH will have the same units as B/H.

 

[tim9000]

In that differentiation I used the derivative of a product rule.

dB/dH will have the same units as B/H.

Ok so the actual working is:
dB/dH = H.dμ(H)/dH + μ(H)*dH/dB

but we don't worry that μ is a function of H, but what happened to the dH/dB, why was that zero?

Ok, so if μ's units are [H/m] but on the graph μ_max is like probably over a Tesla, they've taken liberties with its scale I assume.

 

[NascentOxygen]

Ok so the actual working is:
dB/dH = H.dμ(H)/dH + μ(H)*dH/dB

but we don't worry that μ is a function of H, but what happened to the dH/dB, why was that zero?

Nothing happened to dH/dB, because it isn't there. That term is dH/dH

 

[NascentOxygen]

Going right back to the start ...

You have a graph of B vs H, so why can't you take values of B and divide by the corresponding H to obtain μ?

 

[tim9000]

Going right back to the start ...

You have a graph of B vs H, so why can't you take values of B and divide by the corresponding H to obtain μ?

Yeah I suppose you're right, I was just thinking it was strange that μ is an inherent property of the material that causes be, yet we use B to find it. So I was thinking (not that I achieved it) that there was some expression for μ without B.
Though, how is that term dH/dH ?
I was thinking let u = μ, v = H
d(u.v)/dB = μ*dH/dB + H*dμ/dB

what am I doing wrong?
Thanks

 

[NascentOxygen]

d(u.v)/dH

 

[tim9000]

d(u.v)/dH

OMG, what was I thinking. Thanks!