Aman Chauhan
- 6
- 0
Hi, I have been studying lorentz force . The book says force experienced by a charge in magnetic field is
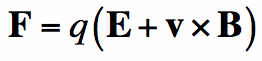
But velocity is a relative concept . In one frame of reference(inertial frame) I might observe the charge moving with some velocity and in the 2nd frame(inertial too) I might observe the charge to be at rest . Does this mean that the force on the particle will be different in the 2 frames? .But since my frames are inertial I should observe the same force on the particle. How is this possible! please help.
But velocity is a relative concept . In one frame of reference(inertial frame) I might observe the charge moving with some velocity and in the 2nd frame(inertial too) I might observe the charge to be at rest . Does this mean that the force on the particle will be different in the 2 frames? .But since my frames are inertial I should observe the same force on the particle. How is this possible! please help.