- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Lorentz Transformation of Fields
- Thread starter sampo
- Start date
In summary: Ohanian, author of "Special Relativity: A Modern Introduction"In summary, the conversation discusses the equations in Michio Kaku's Quantum Field Theory book and the difficulties the reader is having in understanding them. The conversation also touches on the topics of group theory and representation theory, and provides references for further reading. The main focus is on the Lorentz group and its generators, which are used to describe translations, rotations, and boosts in space-time. The conversation includes a visual representation of how these generators work, and explains how they can be used to transform scalar and vector fields.
Physics news on Phys.org
- #2
- 13,349
- 3,122
Wow, a lot of to-the-point questions. I can't use the quote function to try to give an answer to each, because you inserted a picture. Indeed, Kaku's text does not fill in the gaps...
Do you know some group theory and representation theory, so that you'd be able to understand the answer ?
Do you know some group theory and representation theory, so that you'd be able to understand the answer ?
- #3
sampo
- 13
- 0
I can try. I know a little. Give me your best shot, thanks.
- #4
- 13,349
- 3,122
So [itex]\epsilon_{\mu\nu}[/itex] is a set of 6 independent infinitesimal parameters Kaku uses to describe the Lorentz group locally (i.e. in a neighborbood of the identity element). [itex] L^{\mu\nu} [/itex] are then the generators of the connected component of the identity and can be taken as generators (basis elements) in the Lie algebra of the (restricted or full, doesn't matter) Lorentz group.
His first equation is axiomatic, it is the definition of the vector field in terms of its behavior under a restricted Lorentz transformation.
The explicit form of L's (with x and space-time derivatives) is valid in the case of scalar fields, because the spin of the field (angular momentum in the rest frame) is disregarded.
By physical reasons, U([itex] \Lambda [/itex]) is a unitary operator acting on the representation space of the restricted Lorentz group (actually a double cover of the restricted Poincare group), so by Stone's theorem, the L's should be (essentially) self-adjoint.
The calculation for the derivative of L([itex] \Lambda [/itex]) is wrong, as L depends on x and captures the implicit dependence of the U operator on x.
As for point 3), indeed, it's an Euler-MacLaurin series. Turns out that the epsilons are anti-symmetric.
Point 4) a) can be postulated (see above). b) Yes, all vectors have 4 space-time components. c) All fields, well, you move from the Lorentz group to the spin (1,3) group (SL(2,C)), so that spinorial fields will enter the picture.
This is off the top of my head. I can give you references such as Weinberg, Vol.1 or axiomatical field theory texts such as: Streater & Wightman (PCT, Spin-Statistics and All That) or better Bogolubov, Logunov, Todorov (1975 better than 1990).
His first equation is axiomatic, it is the definition of the vector field in terms of its behavior under a restricted Lorentz transformation.
The explicit form of L's (with x and space-time derivatives) is valid in the case of scalar fields, because the spin of the field (angular momentum in the rest frame) is disregarded.
By physical reasons, U([itex] \Lambda [/itex]) is a unitary operator acting on the representation space of the restricted Lorentz group (actually a double cover of the restricted Poincare group), so by Stone's theorem, the L's should be (essentially) self-adjoint.
The calculation for the derivative of L([itex] \Lambda [/itex]) is wrong, as L depends on x and captures the implicit dependence of the U operator on x.
As for point 3), indeed, it's an Euler-MacLaurin series. Turns out that the epsilons are anti-symmetric.
Point 4) a) can be postulated (see above). b) Yes, all vectors have 4 space-time components. c) All fields, well, you move from the Lorentz group to the spin (1,3) group (SL(2,C)), so that spinorial fields will enter the picture.
This is off the top of my head. I can give you references such as Weinberg, Vol.1 or axiomatical field theory texts such as: Streater & Wightman (PCT, Spin-Statistics and All That) or better Bogolubov, Logunov, Todorov (1975 better than 1990).
Last edited:
- #5
sampo
- 13
- 0
Excellent, thank you very much for the great reply. I am currently brushing up on my group theory. I imagine I will have a follow-up question, but while I continue to digest everything, I just wanted to say thanks!
I think one of my problems was how I was thinking of the Lorentz Group as a set of 4x4 matrices with real values, where I guess there is a representation in terms of the L operator. I estimate this is where my question will be, though I don't think I can formulate it yet.
I think one of my problems was how I was thinking of the Lorentz Group as a set of 4x4 matrices with real values, where I guess there is a representation in terms of the L operator. I estimate this is where my question will be, though I don't think I can formulate it yet.
- #6
- 13,349
- 3,122
The Lorentz group IS (isomorphic to) a group of 4x4 matrices with real entries...
- #7
Hans de Vries
Science Advisor
Gold Member
- 1,091
- 27
[itex]L^{\mu\nu}[/itex] contains the three generators of rotation [itex]J^i[/itex] and the three generators of boosts [itex]K^i[/itex].
They form the Poincaré generators together with the four translation operators.
[tex]
\begin{aligned}
& P^\mu &=~& -i\Big( ~~~~~~~~~-\frac{\partial}{\partial x^\mu} &\Big)&
~~~\mbox{4 translation generators} \\
& J^i &=~& -i\Big(\, ~~~~x^j\frac{\partial}{\partial x^k}-x^k\frac{\partial}{\partial x^j} &\Big)&
~~~\mbox{3 rotation generators}~~~~~~ \\
& K^i &=~& -i\Big( ~ - x^i\frac{\partial}{\partial x^o}-x^o\frac{\partial}{\partial x^i} &\Big)&
~~~\mbox{3 boost generators}~~~~~~
\end{aligned}
[/tex]
In the image below you can see how they work. The [itex]\delta[/itex] here is an infinitesimal small parameter.
You can for instance translate an arbitrary function over an infinitesimal small distance by
subtracting [itex]\delta\partial f/\partial x[/itex] (The red and blue delta functions)
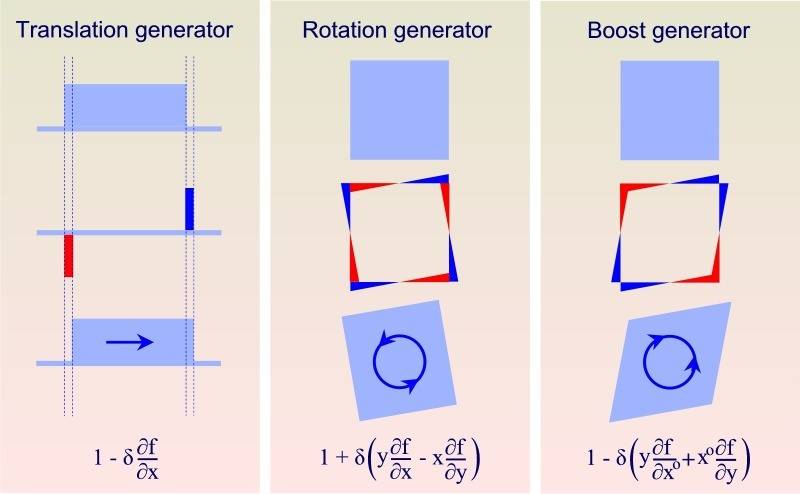
If you repeatedly apply the [itex](1-\delta\partial_x f)[/itex] operator then this amounts to an exponential function like
the one in your book. To translate over a distance [itex]\ell_x[/itex] to the left you do:
[tex]
\exp\left(\,i\ell_x P^x\right)\,f(x) ~=~
\left\{1 +
\frac{\ell_x }{1!}\,\frac{\partial }{dx } +
\frac{\ell_x^2}{2!}\,\frac{\partial^2}{dx^2} +
\frac{\ell_x^3}{3!}\,\frac{\partial^3}{dx^3} +
\cdots\right\}f(x)
[/tex]
The right hand side is just the standard Taylor series. If we write [itex](x-a)[/itex] for the displacement [itex]\ell_x[/itex] and
let the operators act on [itex]f(a)[/itex] then we get the familiar expression for the Taylor series.
[tex]
f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots
[/tex]
The rotate and boost operators work in just the same way. The matrix [itex]\epsilon_{\mu\nu}[/itex] contains the three angles
by which you want to rotate and the three rapidities by which you want to boost just like [itex]\ell_x[/itex] is the
distance by which you want to translate.
The above rotates/boosts works on a scalar field, that is they handle the coordinate transformation.
If you want to transform a (four) vector field then have to operate on the (four) vector parameters
as well because the vector transforms under a general Lorentz transformation.
Hans
They form the Poincaré generators together with the four translation operators.
[tex]
\begin{aligned}
& P^\mu &=~& -i\Big( ~~~~~~~~~-\frac{\partial}{\partial x^\mu} &\Big)&
~~~\mbox{4 translation generators} \\
& J^i &=~& -i\Big(\, ~~~~x^j\frac{\partial}{\partial x^k}-x^k\frac{\partial}{\partial x^j} &\Big)&
~~~\mbox{3 rotation generators}~~~~~~ \\
& K^i &=~& -i\Big( ~ - x^i\frac{\partial}{\partial x^o}-x^o\frac{\partial}{\partial x^i} &\Big)&
~~~\mbox{3 boost generators}~~~~~~
\end{aligned}
[/tex]
In the image below you can see how they work. The [itex]\delta[/itex] here is an infinitesimal small parameter.
You can for instance translate an arbitrary function over an infinitesimal small distance by
subtracting [itex]\delta\partial f/\partial x[/itex] (The red and blue delta functions)
If you repeatedly apply the [itex](1-\delta\partial_x f)[/itex] operator then this amounts to an exponential function like
the one in your book. To translate over a distance [itex]\ell_x[/itex] to the left you do:
[tex]
\exp\left(\,i\ell_x P^x\right)\,f(x) ~=~
\left\{1 +
\frac{\ell_x }{1!}\,\frac{\partial }{dx } +
\frac{\ell_x^2}{2!}\,\frac{\partial^2}{dx^2} +
\frac{\ell_x^3}{3!}\,\frac{\partial^3}{dx^3} +
\cdots\right\}f(x)
[/tex]
The right hand side is just the standard Taylor series. If we write [itex](x-a)[/itex] for the displacement [itex]\ell_x[/itex] and
let the operators act on [itex]f(a)[/itex] then we get the familiar expression for the Taylor series.
[tex]
f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots
[/tex]
The rotate and boost operators work in just the same way. The matrix [itex]\epsilon_{\mu\nu}[/itex] contains the three angles
by which you want to rotate and the three rapidities by which you want to boost just like [itex]\ell_x[/itex] is the
distance by which you want to translate.
The above rotates/boosts works on a scalar field, that is they handle the coordinate transformation.
If you want to transform a (four) vector field then have to operate on the (four) vector parameters
as well because the vector transforms under a general Lorentz transformation.
Hans
Last edited:
What is the Lorentz Transformation of Fields?
The Lorentz Transformation of Fields, also known as the Lorentz Force Transformation, is a mathematical framework that describes how electric and magnetic fields transform under the effects of special relativity. It is a key concept in understanding the electromagnetic force and its behavior in different reference frames.
What is the significance of the Lorentz Transformation of Fields?
The Lorentz Transformation of Fields is significant because it helps us understand how electromagnetic fields behave in different reference frames, and allows us to make accurate predictions and calculations in different frames of reference. It is also a fundamental concept in special relativity and plays a crucial role in many areas of physics, including particle physics and cosmology.
How is the Lorentz Transformation of Fields related to Maxwell's equations?
The Lorentz Transformation of Fields is closely related to Maxwell's equations, which describe the behavior of electric and magnetic fields. In particular, the equations for electric and magnetic fields are not invariant under Lorentz transformations, which means that they must be modified to accurately describe the behavior of these fields in different reference frames.
What is the difference between the Lorentz Transformation of Fields and the Lorentz Transformation of Coordinates?
The Lorentz Transformation of Fields and the Lorentz Transformation of Coordinates are two different mathematical frameworks. The Lorentz Transformation of Fields describes how electric and magnetic fields transform under special relativity, while the Lorentz Transformation of Coordinates describes how the coordinates of an event or object change when observed from different reference frames. Both transformations are important in understanding the effects of special relativity, but they serve different purposes.
What are some applications of the Lorentz Transformation of Fields?
The Lorentz Transformation of Fields has many practical applications, including in particle accelerators, where it is used to calculate the trajectories of particles moving at high speeds. It is also used in the design and operation of various technologies, such as MRI machines and particle detectors. Additionally, the theory of electrodynamics, which is based on the Lorentz Transformation of Fields, is essential in understanding the behavior of light and electromagnetic waves.
Similar threads
- Replies
- 31
- Views
- 3K
-
Quantum Physics
- Replies
- 2
- Views
- 1K
-
Quantum Physics
- Replies
- 3
- Views
- 2K
- Replies
- 101
- Views
- 3K
-
Quantum Physics
- Replies
- 6
- Views
- 1K
-
Quantum Physics
- Replies
- 11
- Views
- 936
-
Quantum Physics
- Replies
- 32
- Views
- 510
-
Special and General Relativity
- Replies
- 18
- Views
- 2K
-
Quantum Physics
- Replies
- 5
- Views
- 756
-
Quantum Physics
- Replies
- 10
- Views
- 2K
Share:
