- #1
JD_PM
- 1,131
- 158
- TL;DR Summary
- I would like to understand and discuss the mathematical formalism of generators (Lorentz Group)
I learned that the Lorentz group is the set of rotations and boosts that satisfy the Lorentz condition ##\Lambda^T g \Lambda = g##
I recently learned that a representation is the embedding of the group element(s) in operators (usually being matrices).
Examples of Lorentz transformations are rotations around the ##x,y## and ##z## axis and boosts in the ##x,y## and ##z## directions. These matrices are thus a particular representation of the Lorentz group.
I've read that the Lorentz group must be independent of any particular representation. Conceptually I understand this should be the case: the representation is simply taking some elements of the whole group.
However, what is not that clear to me is how to show this mathematically.
The book I am reading goes like this: take infinitesimal (Lorentz) transformations and write them in function of infinitesimal angles ##\theta_i## and ##\beta_i##
$$\delta X_0 = \beta_i X_i \tag{10.11}$$
$$\delta X_i = \beta_i X_0-\epsilon_{ijk} \theta_j X_k \tag{10.12}$$
Where ##\epsilon_{ijk}## is the totally antisymmetric tensor. Equations ##(10.11)## and ##(10.12)## can be put together as follows
$$\delta X_{\mu} = i \Big[ \theta_i (J^i)_{\mu \nu} + \beta_i(K^i)_{\mu \nu} \Big] X_{\nu} \tag{10.13}$$
Where I've used Einstein's summation convention.
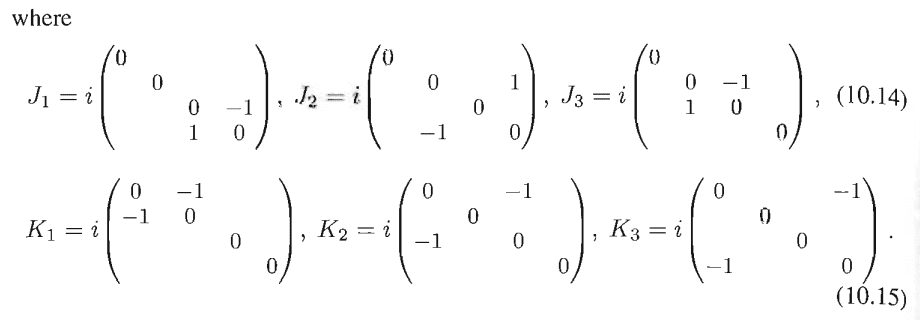
The above matrices are the generators of the Lorentz group. They are labelled as such because any element of the Lorentz group can be uniquely written as
$$\Lambda = \exp(i \theta_i J_i + i \beta_i K_i) \tag{10.16}$$
I'd like to understand from where are ##(10.11)## and ##(10.12)## coming from. Once I do, I may be able to get ##(10.16)##. The only certainty for me is the meaning of ##\beta##; it is the Lorentz factor.
Thank you
Source:
M. D. Schwartz, Quantum field theory and the Standard
Model, Cambridge University Press, Cambridge, New York
(2014).
Section: 10.1.1 Group Theory.
I recently learned that a representation is the embedding of the group element(s) in operators (usually being matrices).
Examples of Lorentz transformations are rotations around the ##x,y## and ##z## axis and boosts in the ##x,y## and ##z## directions. These matrices are thus a particular representation of the Lorentz group.
I've read that the Lorentz group must be independent of any particular representation. Conceptually I understand this should be the case: the representation is simply taking some elements of the whole group.
However, what is not that clear to me is how to show this mathematically.
The book I am reading goes like this: take infinitesimal (Lorentz) transformations and write them in function of infinitesimal angles ##\theta_i## and ##\beta_i##
$$\delta X_0 = \beta_i X_i \tag{10.11}$$
$$\delta X_i = \beta_i X_0-\epsilon_{ijk} \theta_j X_k \tag{10.12}$$
Where ##\epsilon_{ijk}## is the totally antisymmetric tensor. Equations ##(10.11)## and ##(10.12)## can be put together as follows
$$\delta X_{\mu} = i \Big[ \theta_i (J^i)_{\mu \nu} + \beta_i(K^i)_{\mu \nu} \Big] X_{\nu} \tag{10.13}$$
Where I've used Einstein's summation convention.
The above matrices are the generators of the Lorentz group. They are labelled as such because any element of the Lorentz group can be uniquely written as
$$\Lambda = \exp(i \theta_i J_i + i \beta_i K_i) \tag{10.16}$$
I'd like to understand from where are ##(10.11)## and ##(10.12)## coming from. Once I do, I may be able to get ##(10.16)##. The only certainty for me is the meaning of ##\beta##; it is the Lorentz factor.
Thank you
Source:
M. D. Schwartz, Quantum field theory and the Standard
Model, Cambridge University Press, Cambridge, New York
(2014).
Section: 10.1.1 Group Theory.