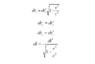SUMMARY
The discussion centers on the distinction between Lorentz transformations and boosts in the context of relative motion in physics. Participants clarify that Lorentz transformations, which include boosts and spatial rotations, do not encompass translations, thus forming the Poincare group when combined with translations. The full symmetry group of Minkowski space is identified as the proper orthochronous Poincare group, represented mathematically by the semidirect product of the Lorentz group and translations. Key equations and properties of these transformations are also discussed, emphasizing the correct application of terminology.
PREREQUISITES
- Understanding of Lorentz transformations and boosts in special relativity.
- Familiarity with the Poincare group and its significance in physics.
- Knowledge of Minkowski space and its geometric properties.
- Ability to interpret and manipulate equations in LaTeX format.
NEXT STEPS
- Study the properties and applications of the Poincare group in theoretical physics.
- Learn about the mathematical formulation of Minkowski space and its implications for spacetime.
- Explore the differences between Lorentz transformations and other transformation types in physics.
- Practice using LaTeX for posting and interpreting equations in scientific discussions.
USEFUL FOR
Physicists, students of theoretical physics, and anyone interested in the mathematical foundations of special relativity and spacetime symmetries.