I Magnet falling though copper pipe

[vanhees71]

I think, the above quoted Youtube video, quoted in #25, is excellent. There it becomes entirely clear, how the "braking effect" comes about, and the student (!) uses the correct terminology, i.e., EMF instead of voltage etc. He also derives the non-relativistic equation of motion and solves them in a quantitative way, using the dipole approximation for the magnet and (tacitly) the quasistationary approximation of electrodynamics.

 

[Orthoceras]

An excellent video, except that it does not explicitly address the special case that I was asking about in my opening post, the case where both the pipe and the return wire (the wire connecting top and bottom of the pipe) have zero resistance. ("Does zero resistance affect the terminal speed of the magnet?") In the case of zero resistance, the average vertical speed of the electrons in the pipe is arbitrary, while the copper atoms are stationary. Then the velocity v from the formula F = k v, in the video at t=21:10, is the difference between the vertical velocity of the magnet and the vertical velocity of the electrons (not the copper atoms). This allows the magnet to fall down to the bottom of the pipe, its lowest energy level.

 

[hutchphd]

This is asked and answered.
There was no mention of a return wire in your original post.
I am finished here. Good luck

 

[rude man]

Ah, then in #27 I meant only the magnetic part of the Lorentz force, $$\vec{F}= q (\vec{v} \times \vec{B})$$, where B is the magnetic field of the magnet.

Yes, that's what I meant too. But the $q \bf E$ part is irrelevant here too, since that component is directed along the E fields you showed in your diagram, not axially. It's what makes the electrons flow circumferentially in the pipe.

The magnetic part of the Lorentz force is downward, if the magnet is falling downward.

Unfortunately, still wrong as I tried to explain.

 

[Swamp Thing]

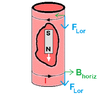
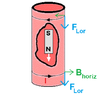
The Lorentz force is (in SI units)
$$\vec{F}=q (\vec{E}+\vec{v} \times \vec{B}).$$

If I'm not mistaken, the OP is referring to the fact that $\vec{v}$ is the resultant of the magnet's velocity in the lab frame and the electrons' velocity within the metal due to the current flow induced by the magnet. Or, to make things a bit simpler, it may help to consider that the magnet is stationary and the tube is moving -- in which case $\vec{v}$ is the resultant of the tube's velocity (which is shared by the electrons) and the velocity of the electrons within the tube, which is tangential to the circumference.

This leads to a question that naturally arises for a naive but interested non-expert like myself:

"If a moving magnet causes an electron to acquire a certain additional relative velocity component due to Lorenz force, then does that newly acquired relative velocity component result in a new extra component of the Lorenz force? Or is everything factored in already?"

To me it seems that this question could possibly underlie the OP's problem and its resolution. If the answer to the above question is "no, there is no new component of Lorenz force", then we need look no further, and this discussion could be closed. If the answer is "yes, there is one", then we still need to explain what keeps the electrons from moving under that extra component of Lorenz force, because in our case that component would be along the tube's axis. (the $F_{Lor}$ in post #27) .Such an explanation may possibly be found in post #25, first paragraph... I don't understand it entirely, but that could be just me.

As for the video, it is excellent, but it seems to presuppose that the tube can be considered as a series of ring-shaped slices, and that the electrons remain within their respective original slices during the whole process. This assumption may well be perfectly valid, but the question of "why" is, I think, not addressed? Not addressed either is the question of, what would happen if we provided the right conditions for the electrons to move downwards under the extra $F_{Lor}$ component, i.e. travel down the tube from slice to slice? Would these conditions not be facilitated if we provided an external path for charges to return from the bottom to the top?

 

[vanhees71]

An excellent video, except that it does not explicitly address the special case that I was asking about in my opening post, the case where both the pipe and the return wire (the wire connecting top and bottom of the pipe) have zero resistance. ("Does zero resistance affect the terminal speed of the magnet?") In the case of zero resistance, the average vertical speed of the electrons in the pipe is arbitrary, while the copper atoms are stationary. Then the velocity v from the formula F = k v, in the video at t=21:10, is the difference between the vertical velocity of the magnet and the vertical velocity of the electrons (not the copper atoms). This allows the magnet to fall down to the bottom of the pipe, its lowest energy level.

I don't know which return wire you are talking about. Of course, the naive limit of zero resistance doesn't make any sense. If you want to treat the problem for a superconducting pipe, you have to employ the correct constitutive relations as for any material, i.e., on the classical level you have to use the London equations

https://en.wikipedia.org/wiki/London_equations

 

[Orthoceras]

I was just trying to understand the vertical forces, in a classical way. Basically comparing the heavy magnet sinking through a fluid of electrons to a heavy object sinking through water. Where I said "zero resistance", "very low resistance" would do just as well, it is not a fundamental thing. The video and the discussion helped me understand that the main vertical force is viscous, and that it depends on the vertical speed of the magnet relative to the electrons. While the electrons exert an upward viscous force on the magnet, the magnet exerts an equally large downward force on the electrons.

The return wire was a just simple way make the vertical motion of the electrons independent of the immobile copper atoms.

 

[gary350]

Falling magnet in a copper pipe is no different than copper wires passing a magnet in a generator. When electricity is generated in copper wires of a generator the generator becomes much harder to turn. Same thing happens in a falling magnet inside a pipe. There are several videos on Youtube. The strangest video is the magnet that was pushed very fast across a table at a piece of copper. The fast moving magnet came to a stop before it slammed into the copper.

 

[Swamp Thing]

If we connect a battery across the copper tube and send a current along its length, will the corresponding electron drift velocity add / subtract from the terminal velocity of the magnet falling through the tube?

 

[hutchphd]

To the degree that the resistivity of the copper is constant wth the added current , it will affect the terminal velocity not at all.

 

[rude man]

No, because there is no B field induced inside the tube. Also, even if there were, it would not generate an axial force.

 

[Swamp Thing]

If we connect a battery across the copper tube and send a current along its length, will the corresponding electron drift velocity add / subtract from the terminal velocity of the magnet falling through the tube?

it will affect the terminal velocity not at all.

No, because there is no B field induced inside the tube. Also, even if there were, it would not generate an axial force.

Perhaps this is one of those things worthy of a nice explanation from the likes of Steve Mould or Veritasium. (Or maybe from Atoms and Sporks). As a reasonably informed and interested layman, I would enjoy learning how my intuition is going wrong.

Intuitively, I have this picture in mind: I think of the current along the pipe as a river, and I think of the bulk of the tube as analogous to the river bank. The magnet is coupled to the electrons, so it's analogous to a boat in the river (although not literally in contact). So it seems to me that the terminal velocity of the boat would be fixed (through the physics of the interaction) with respect to the water, and not with respect to the bank. Hence if there is a relative velocity between the water and the bank, then the terminal velocity of the boat wrt the bank would be the resultant of boat-wrt-water and water-wrt-bank.

Again, I'm not insisting that this picture will predict correctly the result of an experiment, but I do think that the necessary correction to my thought process will be interesting to other laypeople, and may make a good popular exposition. My guess is that it's not a trivial or obvious thing, at least at the level of popular science.

 

[rude man]

Analogies may be well and good for the layman but not if you want to understand physics which is all based on experiments - irrefutable experiments.

 

[hutchphd]

I appreciate that you realize the idea may be flawed, but this is an unfair request. There is nothing to point to. Wolfgang Pauli famously described an idea as "not even wrong" but I will say two things and no more
Electric Fields do not ab initio attract magnets.
Magnetic forces are at right angles to velocity.

 

[DaveE]

So, that's a nice sounding analogy. But how will you know if it actually describes what things do in the real world?

There are some problems that you just really can't do very well based only on popular science. There is a reason physicists take a lot of physics classes.

 

[Orthoceras]

But how will you know if it actually describes what things do in the real world?

Maybe by measuring the voltage between the top and bottom of the pipe. The force F_Lor pushes the electrons down, so theoretically a voltage is to be expected.

 

[mohamed_a]

Analogies may be well and good for the layman but not if you want to understand physics which is all based on experiments - irrefutable experiments.

His problem is in understanding why electrons are not moving with the magnet (let's call it the large/main magnet) i,e, along the direction of its motion, since basic science books refer to electron spinning as electrons being "tiny magnets ", so he is wondering why these tiny magnets are not falling with the main large magnet in the cavity of the pipe because normally magnets align in such a way that they attract and follow the motion of each other. Then he comes to a conclusion that maybe the electrostatic forces and imbalance produced by the imaginative motion of electrons hinders their motion and thus causes the opposing force acting on the large magnet. @hutchphd That's why he is asking if a wire is connected to both ends of the pipe would that cause the electron reserve in the (return /added wire) displace the ones in the pipe material that want to move with the magnet and thus the lenz phenomenon would vanish?.

He basically wants to know why is it copper that resist magnetic field changes and not iron or any other metal

@Orthoceras, Am I right?

 

[Swamp Thing]

Basic science books refer to electron spinning as electrons being "tiny magnets ", so he is wondering why these tiny magnets are not falling with the main large magnet in the cavity of the pipe

No, that's not really what I'm asking. I do realize that the retarding force that slows down the magnet is a result of eddy currents that are induced by the falling magnet. And those eddy currents flow along the circumference of the tube. These eddy currents form, so to speak, a single-turn electromagnet that repels the falling magnet, hence retarding its motion. So far, so good... I hope.

Now my question is more like this... Let the terminal velocity of the magnet in the usual scenario be $V_t$. Now let the whole tube move upwards at a velocity $0.1 V_t$. I would now expect the terminal velocity to be $V_t$ with respect to the tube , but $0.9 V_t$ respect to the lab. Again, so far so good... I hope.

Finally, here's my possibly incorrect conclusion: "It should not matter whether that $0.1 V_t$ happens to be the velocity of the tube moving along with the electrons (as in the last paragraph), or it happens to be the velocity of the electrons alone, with the tube kept fixed (with the electrons being driven upwards by a battery at velocity $k V_t$)".

IMHO, the resolution to my wrong conclusion would be interesting and intriguing to many people with approximately my level of physics. And I'm hoping that it can be explained in an accessible way in the style of Steve Mould et al.

 

[hutchphd]

Finally, here's my possibly incorrect conclusion: "It should not matter whether that 0.1Vt happens to be the velocity of the tube moving along with the electrons (as in the last paragraph), or it happens to be the velocity of the electrons alone, with the tube kept fixed (with the electrons being driven upwards by a battery at velocity kVt)".

Why should it not matter?
It does matter. Something attracted to the electron will likely be repelled by the proton and vice versa. Claims require proof, and yours is an extraordinary claim

 

[Swamp Thing]

Something attracted to the electron will likely be repelled by the proton and vice versa.

Please correct me if I'm wrong, but the eddy current electrons are (magnetically) repelling the magnet, not attracting it? That is, the eddy currents form a single-turn electromagnet with its (e.g.) North pole facing the approaching North pole of the magnet?

If this is correct, then then the protons can't exert an opposing attractive force, because they aren't circulating in a current and hence can't exert magnetic forces? In other words, the protons aren't cutting through the magnetic field in the same way that the electrons are, hence no attractive magnetic force.

 

[Orthoceras]

@Orthoceras, Am I right?

No, I don't think of electrons as being tiny magnets. My idea is rather plain, and it is best summarized by the image below. The force F_Lor pushes the electrons down. I don't think the controversy in this thread has much to do with my idea, the controversy just got a life of its own.

 

[DaveE]

No, I don't think of electrons as being tiny magnets. My idea is rather plain, and it is best summarized by the image below. The force F_Lor pushes the electrons down. I don't think the controversy in this thread has much to do with my idea, the controversy just got a life of its own.
View attachment 296384

The electrostatic repulsion between conduction band electrons is powerful. I don't think they can move to the bottom in a metal tube and collect there to any significant degree. Maybe a bit near the magnet as it falls, but that equilibrium will be established very quickly and will be hard to "see".

 

[Swamp Thing]

Sorry Orthoceras, I didn't notice that mohamed_a's question was directed to you as the OP... Since my posts were the most recent activity on the thread (after some long inactivity), I sort of thought he was asking me.

That said, the general tone of the discussion has been a bit dismissive about your original question, whereas to me it still feels pretty intriguing and I find myself thinking about it now and then.

 

[hutchphd]

Saying something is incorrect is "dismissive" of necessity.
The fundamental point here is that any solid contains both plus and minus charges. The structure maintains its integrity because they interact strongly. To deal only with the electrons, particularly when the mass matters will take you to a wrong place. Also the classical picture of conduction works for a limited subset of circumstances. The anomalously high conductivity of metals was one of the reasons QM was important.
/

 

[vanhees71]

Well, nevertheless the Drude model is qualitatively not too bad. In this simple classical picture you can consider a metal as consisting of a positively charged lattice of ions with the conduction electrons moving quasi-freely within this lattice. Due to (thermal) lattice vibrations and other "defects" the conduction electrons are also scattered, leading to a friction force. Since for usual household currents and of course also for the here considered situation of a magnet falling through a cylindrical-shell conductor the drift velocities are very tiny (order of 1mm/s) the usual "Stokes friction" (friction linear in the momentum of the electron) is good enough, and this leads to the usual constitutive equation $\vec{j}=\sigma \vec{E}$ (neglecting the Hall effect, which must be reintroduced if you want a relativistic description, which however here is completely irrelevant).

 

[hutchphd]

But the Drude model foundational assumption of quasi-free electron transport in the lattice makes no sense in a classical context. And for electrons in that periodic structure the notion of momentum is supplanted by "crystal momentum" which requires the presence of the massive periodic structure. So notions of momentum conservation of the electrons are fraught. That being said I do often think of electrons as little blue Drudish spheres...

 

[vanhees71]

Well, you can do everything quantum theoretically with a very similar qualitative result ;-).

 

[hutchphd]

Yes I like the blue electrons in my head ! But neglecting the background periodicity and the comcommitant surrender of rigorous momentum conservation leads directly to the incorrect analysis here. It is a very useful model, except where it isn't...

 

[vanhees71]

Of course momentum is not conserved, because there are forces acting on the electron. It's an effective description of the underlying microscopic many-body dynamics, and it's amazingly good. Of course, as with any effective model, the parameters are not predicted from first principles but taken as parameters to be determined empirically (in this case electric conductivity).

 

[hutchphd]

Of course they are not free in reality. But it seems to me that the major source of confusion for the OP is the assumption that conduction electrons are "free" particles until they hit the end of the conductor. He then uses momentum conservation for the electrons alone (they are, after all, just free Drude particles) to reach some dubious conclusions. It is the model that takes him down this path.