Magnetic field due to displacement current and Ampere's law

[crick]

I have a doubt on this calculation of magnetic field in presence of displacement current. Consider a capacitor of radius $R$ and with plates at distance $d$ being charged: there is a displacement current in it.

Suppose that I want to calculate the magnetic field $B$ at a distance $r < R$ both inside and outside the capacitor.

Consider the two amperian-loops, both of radius $r<R$, one inside and one outside the capcitor.

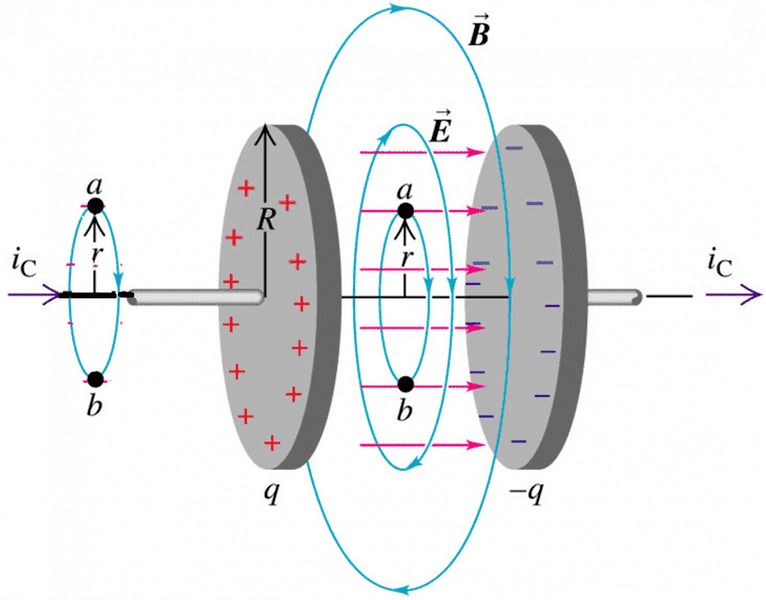
Outside: Ampere Law leads to
$$2 \pi r B= \mu_0 i_C \to B(r)=\frac{\mu_0 i_c}{2 \pi r} \tag{1}$$

Inside: Ampere Law leads to

$$2 \pi rB= \mu_0 \epsilon_0 \frac{\partial \Phi(E(t))}{\partial t}=\mu_0 \epsilon_0 \pi r^2 E(t)\to B(r)=\frac{\mu_0 \epsilon_0 r}{2} E(t)=\frac{\mu_0 \epsilon_0 r}{2d} V(t)\tag{2}$$

Where $V(t)$ is the voltage difference in the capacitor.

Therefore the two different magnetic fields, inside and outside the capacitor are different. Is that right?

I think it is not so strange since $r<R$ and therefore I did not consider all the displacement current, but only a part of it. Or am I missing something important?

 

[phyzguy]

What you have done is correct, except in the second equations your should have dE/dt and dV/dt instead of E and V. But the magnetic field needs to be continuous at r=R. Try setting your two expressions equal at r=R and see what you get. What does this tell you about the relation between i and V?