Magnetic field from four parallel wires

[Niles]

Homework Statement

Hi

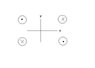
I am looking at four parallel wires of finite length L, whose currents run in the directions shown in the attached figure. There is no gradient along the wire-axis, so from Maxwell's equation
<br /> \frac{dB_x}{dx} = -\frac{dB_y}{dy} \equiv \tilde B.<br />
In order to find an expression for the gradient \tilde B given some current I, I need to use Biot-Savarts law. I think I need to make a binomial expansion for small displacements from the center, but I am not quite sure how to do this with the Biot-Savart law. I would really appreciate a hint.


Niles.

 

[frogjg2003]

Or you could simply superimpose 4 fields from the individual wires. I would imagine you've already solved the field for a single wire, so B=B1+B2+B3+B4. Remember, the wires aren't all in the same direction, so you have to add some and subtract others.

Once you've resolved all your issues https://www.physicsforums.com/showthread.php?t=645327, you should be able to write everything in terms of the x and y components of the 4 wires.