Magnetic field strength for circular loop

[Sho Kano]

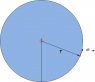
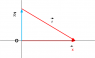
When deriving the magnetic field strength due to a circular loop at some distance away from it's center (using Biot-Savart's law), why is the angle between ds and r 90 degrees?

This is a youtube video with the derivation, see 5:55

 

[BvU]

$\vec {dl}$ is in the $yz$ plane. As drawn it is in the negative $y$ direction, so that $\vec {dl} \perp \vec r$ for the $r$ in the $xz$ plane. From Pythagoras you have $R^2 + x^2 = r^2$. All $\vec r$ have the same length (from symmetry - rotation around the x-axis) - so this $R^2 + x^2 = r^2$ is true for all $\vec r$ -- so all these are rectangular triangles

 

[Hesch]

The 90 degrees comes from the cross product in Biot-Savart's law.

 

[BvU]

@Hesch: I would say the 90 degrees is used to simplify $\vec a\times\vec b$ to $|\vec a||\vec b|$ in BS, not that it comes from BS.

 

[Sho Kano]

$\vec {dl}$ is in the $yz$ plane. As drawn it is in the negative $y$ direction, so that $\vec {dl} \perp \vec r$ for the $r$ in the $xz$ plane. From Pythagoras you have $R^2 + x^2 = r^2$. All $\vec r$ have the same length (from symmetry - rotation around the x-axis) - so this $R^2 + x^2 = r^2$ is true for all $\vec r$ -- so all these are rectangular triangles

r is not pointing straight out of the yz plane, so why is it perpendicular?

 

[BvU]

The $\vec r$ as drawn in the picture is in the xz plane. The $\vec {dl}$ as drawn is perpendicular to the xz plane: it is in the negative y direction. So that $\vec {dl}$ is perpendicular to that $\vec r$.
For all other $\vec {dl}$ (in the yz plane) you can see they are $\perp$ 'their' $\vec R$ and also $\perp$ to the x-axis, so $\perp$ the plane in which their $\vec R$, the x-axis and also $\vec r$.

Bringing in Pythagoras was unnecessary - a mistake on my part.

 

[Hesch]

@Hesch: I would say the 90 degrees is used to simplify ⃗a×⃗b\vec a\times\vec b to |⃗a||⃗b||\vec a||\vec b| in BS, not that it comes from BS

Sorry, maybe it's a danish term.
Try to write something in danish to me. Maybe I will comment it.

 

[Sho Kano]

The $\vec r$ as drawn in the picture is in the xz plane. The $\vec {dl}$ as drawn is perpendicular to the xz plane: it is in the negative y direction. So that $\vec {dl}$ is perpendicular to that $\vec r$.
For all other $\vec {dl}$ (in the yz plane) you can see they are $\perp$ 'their' $\vec R$ and also $\perp$ to the x-axis, so $\perp$ the plane in which their $\vec R$, the x-axis and also $\vec r$.

Bringing in Pythagoras was unnecessary - a mistake on my part.

So just because yz is perpendicular to xz? There is no way dl is perpendicular to r because r extends from the yz plane down to xy, making an angle that is not 90 degrees.

 

[BvU]

No, not just because yz $\perp$ xz. Because $\hat y \perp$ xz for the situation as drwn in the video. In general:

Point P goes around the ring. At all such P $$ \vec {dl}\perp \vec R \quad \& \quad \hat x \perp \vec {dl} \quad \Rightarrow \quad \vec {dl}\perp (\vec x - \vec R) = \vec r $$

Hesch: jeg forstar lidt Dansk

 

[Sho Kano]

No, not just because yz $\perp$ xz. Because $\hat y \perp$ xz for the situation as drwn in the video. In general:

Point P goes around the ring. At all such P $$ \vec {dl}\perp \vec R \quad \& \quad \hat x \perp \vec {dl} \quad \Rightarrow \quad \vec {dl}\perp (\vec x - \vec R) = \vec r $$

View attachment 100340

Hesch: jeg forstar lidt Dansk

I lost you at dl perpendicular to x - R, why did you do that? And why is it equal to r?

 

[BvU]

dl is perpendicular to $\vec R$
dl is perpendicular to $\hat x$ so dl is perpendicular to $\vec x$
that means dl is perpendicular to the plane in which both $\vec R$ and $\vec x$ lie.
That plane is described by $a\vec x + b \vec R$.
The vector $\vec r$ is $\vec R -\vec x$ so it is in that plane.
Why is $\vec r=\vec x -\vec R$ ?
i don't know how to say that. Perhaps a picture helps ?

 

[Sho Kano]

dl is perpendicular to $\vec R$
dl is perpendicular to $\hat x$ so dl is perpendicular to $\vec x$
that means dl is perpendicular to the plane in which both $\vec R$ and $\vec x$ lie.
That plane is described by $a\vec x + b \vec R$.
The vector $\vec r$ is $\vec R -\vec x$ so it is in that plane.
Why is $\vec r=\vec x -\vec R$ ?
i don't know how to say that. Perhaps a picture helps ?

View attachment 100362

Okay, I see where x - R comes from.

So this is how I'm comprehending it:
dl is pointing outwards (imagine a wire pointing out), so any r from its surface is perpendicular to it.
Before, I was confusing dl with the z vector. The angle that r makes with z will not be perpendicular.

 

[vanhees71]

I think the reason is that they look for field only along the $z$ axis. I guess there the integral can be solved analytically, while the field of the current-conducting circular loop at an arbitrary position leads to elliptic integrals.