Pushoam
- 961
- 53
The above thing is the image.Pushoam said: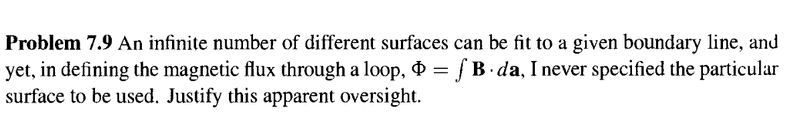
Please click it.
The discussion revolves around the concept of magnetic flux and its calculation in the context of Faraday's law of electromagnetic induction. The original poster references a problem from Griffith's "Introduction to Electrodynamics" regarding the justification of using different surfaces for calculating magnetic flux through a loop.
The discussion is ongoing, with participants providing insights and examples to clarify the concepts. Some have expressed uncertainty about the implications of Griffith's statements regarding non-rectangular loops and varying magnetic fields, while others have suggested that with sufficient information, these calculations are feasible despite their complexity.
Participants note the challenges posed by non-rectangular loops and non-uniform magnetic fields, as well as the assumptions required for applying the flux rule effectively. There is an acknowledgment of the higher mathematical demands in these scenarios.
The above thing is the image.Pushoam said: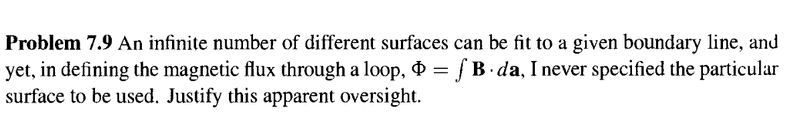
The problem includes the statement " ... I never specified the particular surface to be used ... ". Please include the statement referred to.Pushoam said:The above thing is the image.
Please click it.
OK, thanks. I know the Stokes theorem is appropriate here, but I haven't decided yet on whether the way you invoked the Divergence theorem isn't also OK. That's my answer for the moment & I'll try to get back a bit later with any new views.Pushoam said:I attached the whole section of the book from which the question is asked.The definition of flux is given in page no. 295, first attachment.
rude man said:I know the Stokes theorem is appropriate here,
After looking at your pdf files I see that neither theorem is appropriate for proving that the shape of the surface enscribed by a contour (a loop) is immaterial. I have to apologize to you for going in that direction for so long but i did need to see those pdf pages.Pushoam said:How can one apply stokes' theorem to answer this question ?
Will you please give me some hint?