Magnetic Flux through a Rectangular Loop Due to a Straight Wire

[Bashyboy]

Homework Statement

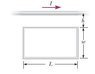
A loop of wire in the shape of a rectangle of width w and length L and a long, straight wire carrying a current I lie on a tabletop as shown in the figure below.

(a) Determine the magnetic flux through the loop due to the current I. (Use any variable stated above along with the following as necessary: μ0 and π.)

(b) Suppose the current is changing with time according to I = a + bt, where a and b are constants. Determine the magnitude of the emf that is induced in the loop if b = 19.0 A/s, h = 1.00 cm, w = 14.0 cm, and L = 1.50 m.

(c) What is the direction of the induced current in the rectangle?

Homework Equations

The Attempt at a Solution

For part (a), the answer involves integrating h to h+w. I honestly do not understand why this is so. Wouldn't this calculation include the flux through the region between the wire carrying the current and the loop? I would certainly appreciate it if someone Could someone explain the rationale that accompanies this calculation.

 

[tia89]

The field around the straight wire has cilindrical symmetry, and you can find it out with the usual formula. It will depend only on the distance from the wire. Now the flux (in case the field is constant) is simply the product of the area and the field, as the field vector and the normal to the area will be parallel (due to the above mentioned cilindrical symmetry) and then the scalar product is simply the product of moduli.

Given this, you are able to compute the flux through an infinitesimal rectangular area at distance $r$ from the wire as
$$ F=B(r)L\mathrm{d}r $$
Now simply integrate this infinitesimal flux where you need it, therefore between $r=h$ and $r=h+w$. In practice what you are doing is to sum all the infinitesimal fluxes internal to the loop you have. And no, to consider also the contribution of the part between the wire and the loofa, you should start integrating at $r=0$.