Why is the magnetic force directed downward in this scenario?

[Amaelle]

Good day All!
while trying to solve this question

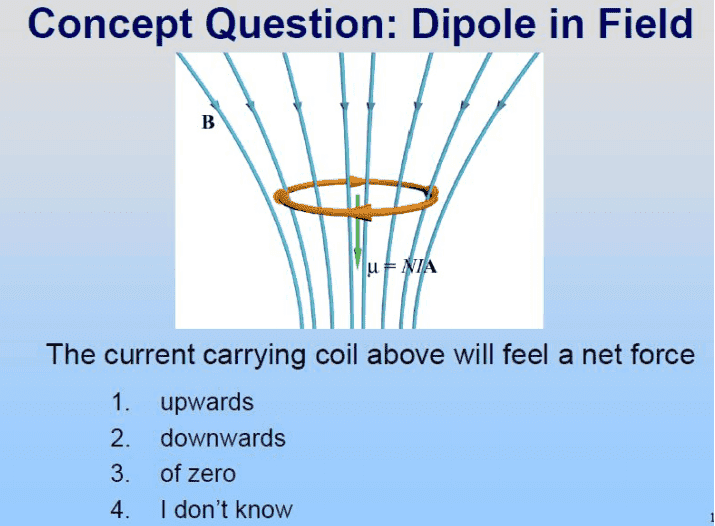
I use the right hand rule and according to it the Force should be directed outward (pointing toward me)
but here is the answer that puzzeld me

I really don't get why it is down , and would feel very grateful if someone can explain me the reason
thanks in advance!

 

[Charles Link]

The way I know how to work this one is to use potential energy $E=-\mu \cdot B$, and use the force $F=-\nabla E$. The first equation comes about because torque $\tau=\mu \times B$ with a $\sin(\theta)$ in the cross product, and the integral of $E=\int \tau \, d \theta$ gives the $\cos(\theta)$ which comes in the dot product $E=- \mu \cdot B$. $\\$ In a uniform magnetic field, a magnetic dipole can experience a torque, but no net force. The force is a result of the non-uniform magnetic field. In simple terms, the equation $E=-\mu \cdot B$ will result in an attraction of a magnetic moment that is aligned with the magnetic field to a region of stronger magnetic field, because the potential energy $E$ at the region of stronger magnetic field is more negative. The second equation $F=-\nabla E$ is a quantitative expression of what I have just described qualitatively. $\\$ Notice also, if the magnetic moment is anti-parallel with the field, the dot product will make $\cos(180^o)=-1$, and the potential energy $E$ will be more positive if you move to a region of stronger magnetic field $B$.

 

[Amaelle]

Thanks a lot!