Magnetic Induction: EMF Function of Time

[xenolalia]

Hi,

I've been thinking about the shape of the voltage waveform induced by a magnet falling through a coil. I know (both intuitively and from empirical experience) that the voltage should become increasingly positive as the magnet approaches the coil, then it should decrease rapidly (intersecting the x-axis as it passes through the coil), finally becoming less and less negative as the magnet falls away from the coil. Of course, "positive" and "negative" could just as easily be reversed, depending on the magnet's orientation.

All this in mind, I've derived an equation for the induced voltage (as a function of time) starting from Faraday's and Lenz's laws. The full derivation is attached.

My question is as follows: why does the graph of the voltage function I end up with (see here) intersect the x-axis at t=0 (the instant that the magnet is dropped) rather than at the instant the magnet passes through the coil (about t=0.45 if dropped from a height of 1 meter)? In other words, why is the positive section of the voltage graph to the left of the y-axis?

Thanks very much!
xenolalia

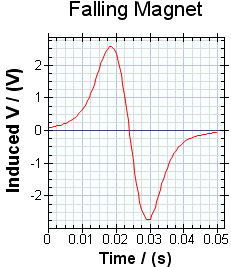
P.S. I was expecting the graph to more or less resemble this:

 

[gsal]

why does the graph of the voltage function intersect the x-axis at t=0?

Because that's precisely the time at which relative motion between coil and magnet start? You know, magnetic lines may be weak but may be reaching the coil...

 

[xenolalia]

Since the coil begins to accelerate toward the magnet at t=0, shouldn't the flux be decreasing (or increasing) rapidly as the magnetic field grows in strength? And because emf is the negative time-derivative of flux, shouldn't the voltage be increasing (or decreasing) rapidly also?

I'm fairly certain that's what actually happens when the experiment is conducted (e.g. http://www.practicalphysics.org/go/Experiment_210.html" ).

 

[Philip Wood]

May I congratulate you on the presentation of your mathematical argument?

It's not the acceleration which controls the rate of change of flux, but the relative velocity of magnet and coil (as well as dB/dr). When you release the magnet it has hardly any velocity, so dB/dt is almost zero. Have I missed something?

 

[xenolalia]

Yes: immediately after the magnet is released its velocity is very small, and therefore its dB/dt should be near zero. Then, as the magnet accelerates, its velocity (and hence, the magnitude of dB/dt) should increase rapidly. However, as the magnet passes through the coil and begins to fall away, the strength of B then begins to decrease rapidly; Lenz's law dictates that the induced current should therefore switch directions to compensate for the increasingly negative dB/dt.

The emf function I have derived has approximately the right shape, but the region of the graph that should correspond to the instant that the magnet falls through the coil seems to be located at t=0. My question is this: why doesn't the graph "start" at the origin? (It is currently "centered" at the origin.)

 

[Philip Wood]

I'm afraid there is a serious problem with your analysis. Sorry I didn't spot this earlier. According to your formula the emf goes to infinity when h =gt²/2. This is when the magnet is passing the centre of the coil (which I'm assuming to be 'flat', i.e effectively in one plane).

This is caused by your use of eq.2 when the magnet is near the coil. Eq. 2 is for B at a point on the axis of the coil. When the magnet is far from the coil, it's a good approximation to say that B has this value all over the cross-section of the coil, so \Phi = BA.

But the lines of flux splay out from the N pole of the magnet and return to the South pole, so when the magnet is near the coil the field won't in general be normal to the plane of the coil, nor uniform in magnitude over the coil area, and indeed the flux may well be threading in one direction through the central part of the coil's cross-section, and returning (i.e. going in the other direction) through the outer zones of the coil's cross-section, as the lines of flux curl round to return to the far pole.

Taking account of this - and of course, it would be quite difficult to do so mathematically - would get rid of the infinity. It would also make your formula for emf much more complicated, though your existing formula is fine for when the magnet is far from the coil.

 

[xenolalia]

I see. Thanks for the explanation! I think if I have to differentiate anything much messier, I'm just going to start using mathematica.

xenolalia

 

[Philip Wood]

It's the integration over the area of the coil that worries me!

 

[Philip Wood]

I expect you've moved on to other things, but I thought I'd report that it's much easier to take account of the 'flux spread' than I'd thought, and to obtain a manageable formula for the emf. I'll give more details if you're still interested - but I'm not expecting you to be: life moves on!