vxr
- 25
- 2
- Homework Statement
- A ladder of length ##l = 8.6 m## long and mass ##m = 60 kg## is placed in nearly vertical position against the wall of a building. You stand on a rung with your center of mass at the top of ladder. As you lean back slightly, the ladder begins to rotate about its base away from the wall. Is it better to quickly step off the ladder and drop to the ground or to hold onto the ladder and step off just before the top end hits the ground? In calculations take your mass.
- Relevant Equations
- ##p = mv, E_{k} = \frac{mv^2}{2}##
So there are two cases:
a). free fall (straight forward for me)
b). ladder rotating and jumping off in last moment (I am interested in trying to understand this case)
I believe I should take into account momentum at the time the man hits the ground in both cases? The smaller, the better. Or should I take into account kinetic energy? Both use mass and velocity.
This is pretty much the b). case:
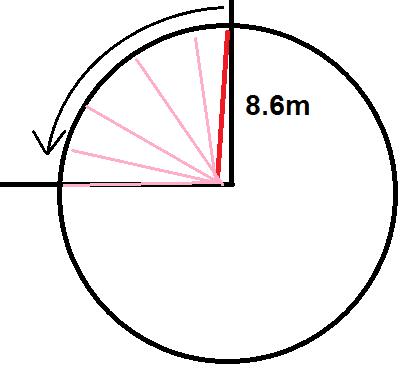
Red is the almost-vertical (assume vertical) ladder, and pink is its movement when it's rotating. Total distance the man standing on top of the rotating ladder travels is ##s = \frac{2\pi r}{4} = \frac{\pi r}{2}##
I need to find final velocity of such system. How do I find it? I think there is no horizontal acceleration, horizontal velocity is constant. On the other hand ##a = g## and vertical velocity is not constant.
Should I use this equation?
##v_{f}^2 = v_{i}^2 + 2as##
##v_{f}^2 = v_{i}^2 + 2gs \quad \land \quad v_{i} = 0##
##v_{f}^2 = 2gs##
##v_{f} = \sqrt{2gs} = \sqrt{g\pi r}##
And when calculating the momentum I should take into account in this case sum of both ladder and a man's mass? Let ##M## be a mass of man.
##p_{f} = (M+m)v_{f}##
##p_{f} = (M+m)\sqrt{g \pi r}##
This seems too simple, I am sure I have made some mistakes, right? Perhaps forgot about some ##v_{x}## or ##v_{y}## components? And/or I shouldn't take into account sum of both masses, because after all the man jumps off of the ladder the very last moment.
Thanks for help.
a). free fall (straight forward for me)
b). ladder rotating and jumping off in last moment (I am interested in trying to understand this case)
I believe I should take into account momentum at the time the man hits the ground in both cases? The smaller, the better. Or should I take into account kinetic energy? Both use mass and velocity.
This is pretty much the b). case:
Red is the almost-vertical (assume vertical) ladder, and pink is its movement when it's rotating. Total distance the man standing on top of the rotating ladder travels is ##s = \frac{2\pi r}{4} = \frac{\pi r}{2}##
I need to find final velocity of such system. How do I find it? I think there is no horizontal acceleration, horizontal velocity is constant. On the other hand ##a = g## and vertical velocity is not constant.
Should I use this equation?
##v_{f}^2 = v_{i}^2 + 2as##
##v_{f}^2 = v_{i}^2 + 2gs \quad \land \quad v_{i} = 0##
##v_{f}^2 = 2gs##
##v_{f} = \sqrt{2gs} = \sqrt{g\pi r}##
And when calculating the momentum I should take into account in this case sum of both ladder and a man's mass? Let ##M## be a mass of man.
##p_{f} = (M+m)v_{f}##
##p_{f} = (M+m)\sqrt{g \pi r}##
This seems too simple, I am sure I have made some mistakes, right? Perhaps forgot about some ##v_{x}## or ##v_{y}## components? And/or I shouldn't take into account sum of both masses, because after all the man jumps off of the ladder the very last moment.
Thanks for help.
Last edited: