Mass Moment of Inertia: slanted solid parallelogram: Well past wit's end

[MikeHoulder]

Perhaps Tensor Calculus holds the answer; but I just can't justify the time for studying that as I know nothing of it.
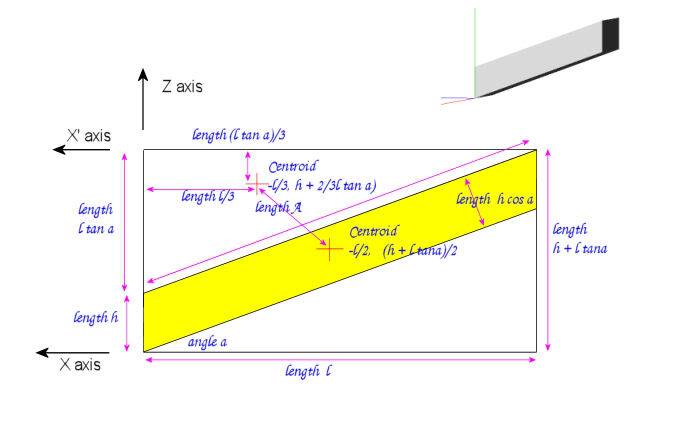
The end objective is to calculate the mass moment of inertia of the yellow solid parallelepiped about rectangular axes through its centre of mass as in the diagram here.

The determining inputs are:
the length of the parallelepiped projected onto the X axis, length l
the angle of slant, angle a
the slant height of the parallepiped, length h
the depth of the parallelepiped, length d
the volume density which is constant

Specimen inputs are:
length l = 10
slant angle a = 10 degrees
length h = 2
depth d = 6
volume density = k

Using the standard formula for the whole rectangular prism about its centre of mass
I_xc = M 1/12 (d² + l² tan²a), I_yc, I_zc similarly

The whole rectangular prism is composed of the target parallelepiped and two triangular wedge shapes.
These wedge shapes are symmetrical about the rectangular centre of mass. So only one of them need be considered.

I could not find any standard formula for a triangular wedge shape. But if the mass moments for this could be found about any rectangular axes, using the parallel and perpendicular axis theorems, the mass moments could be found about the X_c, Y_c, Z_c axes.

Trying to derive these values for the wedge, I always end up with the area moment of a triangle, m.l²/6.
And any attempt to find the mass moment produces inconsistent values.

Please, please, will some kind person sort me out.
Mike

 

[Mindscrape]

If you know the axis of rotation you can just find the moment of inertia about that axis, wohoo. If you don't know the axis of rotation and you are set on using that particular coordinate system then you'll have to fill in your inertia tensor. If you just want to look at the behavior of the parallelepiped then you ought to diagonalize the tensor to its principle axis (rotate it flush with x,y,z). Here's what you need to do to build your tensor:

I_{i j} = \int \int \int_V \rho (\mathbf{r} \cdot \mathbf {r} \delta_{i j} - r_i r_j) dV

 

[MikeHoulder]

Mindscrape, thank you very much for your comment. My fundamental problem is that I am very isolated, millions of miles from anywhere. Do you know of a free course of Vectors and Tensors on Internet that would help me to understand your solution? Failing that, a good shortbook from Amazon?

My problem above centres on finding the mass moment of inertia of a beam with a constant cross-section of a right-angled triangle with the two smaller sides parallel to two axes. The exact point of my problem is/was believing that the area radius of gyration is equal to the mass radius of gyration. I now think it must be so. The old textbook I am using assumes this without stating this or discussing it.

 

[Mindscrape]

Sorry I never got back to you, I didn't realize you responded. In your case you should un-rotate your coordinate axis, to put it simply, so that you can simply do the triple integral of the diagonal elements. Do you know how to do integration? It would look something kind of like this.

\int_{-h/2}^{h/2} \int_{-w/2}^{w/2} \int_{x=m z+b_0}^{x=m z-b_0} \rho r^2 dx dy dz

I don't know about a good source that will give you an all in one package. If I were you I would first try to google inertia tensor examples, and if it's too advanced then you might just have to take your book's word for it.

 

[MikeHoulder]

Thanks a million, Mindscrape. I had derived something like your second integral above. The problem is there are a large number of terms in the solution and so it is not suitable for use as a primitive. So a method of approximation seems to be the best way.

What I want to do is to find an equivalent rectangular prism for a set of primitive elements. I am finding that such an equivalent does not always exist. So again I have to find some approximation method.

My final mathematical objective is to set correctly the torsion spring-damper joint parameters for a complex component. This is to provide better modelling within the German flight simulator, Aerofly.

Your words "In your case you should un-rotate your coordinate axis" are exciting. They imply that the moments of inertia about the centroid are independent of the rotation of the object. Actually, that seems to make a lot of sense. A quick confirmation of that will save me a mountain of grief.

Thank you again
Mike

 

[MikeHoulder]

No, my excitement above must be mis-placed. If the object is rotated with respect to the axes - no. If both axes and object are rotated - yes. But that's pretty useless. I'm going to have to study tensors.
Mike

 

[Mindscrape]

How "independent" the moments of inertia are depend on the symmetry of the object you are looking at. If I have a cone top then we know from symmetry moments about the plane of x-y, where my coordinates refer to if you stand the top upright and use the standard x-y-z orientation, are the same. In the end, we'll end up with two rotations, one of the top, and the other of precession. If everything were symmetrical, like a ball, then there would only be one possible mode of rotation. This should key you into the idea that the Earth isn't fully symmetrical, it actually has a bit of a belly, because we have two different modes of rotation, our spin (the days) and our precession (the seasons).

It's nice to have a diagonalized matrix because your eigenvectors will form a basis such that they are the fundamental components of your inertia space, and the eigenvalues (how much your space transforms) are simply the elements of the diagonalized matrix. I don't know how much linear algebra you've done, so I'll stop my linear algebra talk there.

This mathematica project may help you out to visualize the inertia tensor with different objects. You don't need mathematica unless you want to edit the file, only the mathematica player.
http://demonstrations.wolfram.com/PrincipalAxesOfInertia/

 

[MikeHoulder]

Mindscrape, I've sent you a visitor message. I suggest, very hopefully and without any sort of proof, the following hypothetical theorem:

Let S be the set of all 3D shapes which have at least a uniform cross-section on one axis and/or some degree of symmetry?.
Let T be the set SxMxC where M is scalar corresponding to mass and C is a triple corresponding to the location of the centroid of the element.
Let V be any non-empty subset of T. For any set V, there exists a unique rectangular prism whose centroid is equal to the centroid of the composed elements of V and whose mass moments of inertia are equal to those of the composed elements of V.

It does seem to be true in some simple cases. Otherwise, all I've got so far seem to be counter-examples. But of these, I believe my calculations of their moments of inertia are incorrect. Does such a theorem exist? What restrictions on S are necessary to make the theorem true?

Mike