Mass on a spring from equilibrium

AI Thread Summary
The discussion centers on the use of the formula Fs = 1/2 kx^2 in relation to a mass on a spring and its equilibrium position. The confusion arises over why x is taken as 0.1m instead of 0.05m, given that 0.05m is the displacement from equilibrium. The key point is that the formula measures energy based on the spring's extension from its unstretched position, not from equilibrium. Therefore, x should represent the total extension from the unstretched state. Understanding this distinction clarifies the application of the formula in calculating spring energy.
mancity
Messages
26
Reaction score
2
Homework Statement
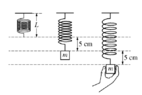
An object with mass m is suspended at rest from a spring with a spring constant of 200 N/m. The length of the spring is 5.0 cm longer than its unstretched length L, as shown above. A person then exerts a force on the object and stretches the spring an additional 5.0 cm. What is the total energy stored in the spring at the new stretch length?
Relevant Equations
Fs=1/2kx^2
Can someone explain that, when using the formula (Fs=1/2 kx^2) why do we use x=0.1m instead of 0.05m? Seems like a simple concept but why isn't it 0.05m (since 0.05m from equilibrium). Thanks.
 

Attachments

  • Screen Shot 2023-12-22 at 5.47.39 PM.png
    Screen Shot 2023-12-22 at 5.47.39 PM.png
    9.3 KB · Views: 79
Physics news on Phys.org
If you use the formula ##E=\frac{1}{2}kx^2##, the reference for energy (zero energy) is the position with the spring unstretched. So, you need the extension of the spring relative to the unstretched position.
 
Reply
  • Like
Likes MatinSAR and mancity
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Simple harmonic motion equation
Replies
3
Views
1K
Irodov- 1.123- Simple conceptual question with two masses connected by a spring
Replies
20
Views
553
Force of spring equation problems
Replies
4
Views
2K
Force transmitted to a block in viscous fluid through a spring, cord, and pulley
Replies
6
Views
772
Finding a formula for displacement of a mass on a spring using v.
Replies
2
Views
622
Spring with mass hangs from the ceiling
Replies
22
Views
1K
Conservation of Energy with springs
Replies
13
Views
1K
Springs and Pulleys - Force analysis
Replies
18
Views
1K
Stretching of a rotating spring
Replies
8
Views
2K
Finding the damping force for a critically damped oscillator
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top