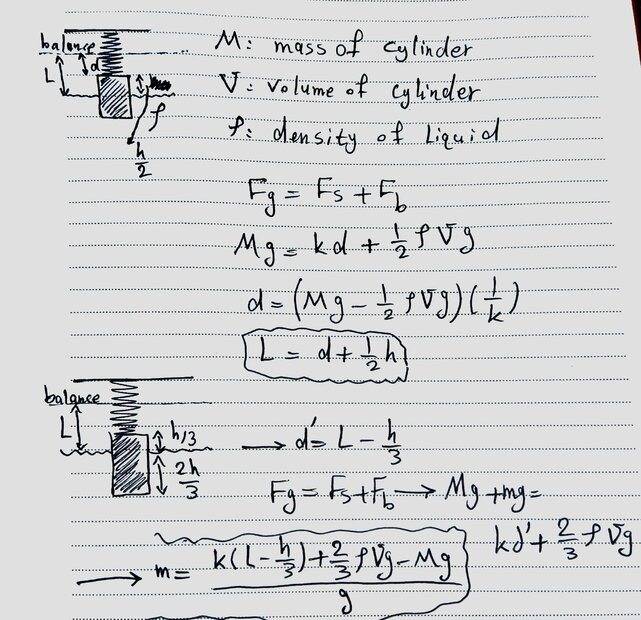SUMMARY
The discussion centers on the physics of a mass on a spring that is semi-submerged in a liquid. The participants explore the relationship between variables such as spring constant (k), height (h), fluid density (ρ), gravitational acceleration (g), and volume (V). The conclusion reached is that the definitions of the variable d can be adjusted, yet they yield equivalent results when substituting into the equations governing the system. The emphasis is on the correct application of these variables to derive the same outcome.
PREREQUISITES
- Understanding of Hooke's Law and spring mechanics
- Basic principles of fluid mechanics
- Knowledge of gravitational forces and buoyancy
- Familiarity with algebraic manipulation of equations
NEXT STEPS
- Study the principles of buoyancy and Archimedes' principle
- Learn about the mathematical modeling of oscillatory motion in fluids
- Explore the effects of damping in spring systems submerged in liquids
- Investigate the relationship between spring constants and fluid density
USEFUL FOR
Physics students, mechanical engineers, and anyone interested in the dynamics of oscillating systems in fluid environments.