Mass on inclined plane, string has mass

[deekin]

Homework Statement

A block of mass M has a string of mass m attached to it. A force F is applied to the string and it pulls the block up a frictionless plane inclined at angle θ to the horizontal. Find the force the string exerts on the block.

Homework Equations

F = ma

The Attempt at a Solution

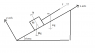
I have uploaded a picture of the free body diagram. My first problem is, what is the force that is keeping the string up? The mass M has the normal force from the inclined plane, and intuitively I know it is the tension in the string that keeps it from moving downwards due to the force mg.

So I first started with finding the forces acting on the string.

F_x= F - mgsinθ - Mgsinθ = ma
F_y= -mgcosθ + ?? = 0

Now the block:

F_x= F_string - Mgsinθ = Ma
F_y= N - Mgcos = 0

I assumed the acceleration for both is the same. So I used the force in the x direction of the string to solve for a.

a = (F/m) - gsinθ - (Mg/m)sinθ

Now we use the force in the x direction for the block.

F_string - Mgsinθ = M((F/m) - gsinθ - (Mg/m)sinθ) = (MF/m) - Mgsinθ - (M²g/m)sinθ

Then we have
F_string = (MF/m) - (M²g/m)sinθ.

What I would like to know is, am I missing something? This problem was assigned in my upper division Classical Mechanics class (we're using Analytical Mechanics by Fowles and Cassiday). I've never had to do a problem where the string had mass. I went and asked the professor if there was some sort of trick or something, and he said no, just treat the problem like you would in General Physics 1.

 

[Chestermiller]

The x force balance on the block is correct, but the x force balance on the string is incorrect. The string tension varies from one end of the string to the other. At one end, the tension is F. At the other end it is F_String. So the x force balance on the string should be:

F - mgsinθ - F_String = ma

You can add the two x force balances together and eliminate F_String to get the acceleration. You can then find F_String from the x force balance on the block.

Chet

 

[deekin]

Thank you.

So using the above suggestion, for the forces in the x-direction for the string, I have

F - mgsinθ - F_string = ma

Now I add this to the expression for the force in the x-direction for the block and get

F - mgsinθ - Mgsinθ = (M + m)a

so solving for the acceleration, we get

a = (F - (M + m)gsinθ)/(m + M).

Then plugging this in, we get

F_string - Mgsinθ = M(F - (M + m)gsinθ)/(m + M)

Which means

F_string = MF/(m + M).

If I have missed something else, please let me know. Thank you so much for your help.

 

[Chestermiller]

Thank you.

So using the above suggestion, for the forces in the x-direction for the string, I have

F - mgsinθ - F_string = ma

Now I add this to the expression for the force in the x-direction for the block and get

F - mgsinθ - Mgsinθ = (M + m)a

so solving for the acceleration, we get

a = (F - (M + m)gsinθ)/(m + M).

Then plugging this in, we get

F_string - Mgsinθ = M(F - (M + m)gsinθ)/(m + M)

Which means

F_string = MF/(m + M).

If I have missed something else, please let me know. Thank you so much for your help.

Looks good. Now, in your equation for a, divide each of the two terms in parenthesis by (m+M) to see a more clear cut version for a.
Also, looking at your final result, is there any simple interpretation you might be able to provide to this result?

Chet

 

[deekin]

The only simple interpretation that I can come up with is that the force that the string exerts on the block is less than the force F that is acting on the string.

Thanks so much for your help, Chet.

 

[Chestermiller]

The only simple interpretation that I can come up with is that the force that the string exerts on the block is less than the force F that is acting on the string.

Thanks so much for your help, Chet.

According to your correct results, the mass of the string can kind of be lumped together with the mass of the block. It shows that M/(M+m) of the force F goes into accelerating the block and m/(M+m) goes into accelerating the string (the difference between F and F_string).

Chet