mancity
- 26
- 2
- Homework Statement
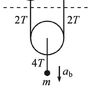
- Consider the triple Atwood’s machine shown in Fig. 4.21. What is the acceleration of the
rightmost mass?
- Relevant Equations
- torque=I alpha=rF => F_rot = 1/2 mr * alpha
Say you had a pulley with a mass hanging off of it, like in the picture. What I don't understand is, what idealizations are being made such that there is no net torque being generated? My confusion is that we have a massive pulley, hence there will be rotational inertia. But it is pretty clear that in this diagram there is no net torque that resists the acceleration of the pulley. Thanks