Mass Spring Damper system with opposing springs

[helium4amc]

I'm sure I must be being a bit dim here, but I can't work this out!

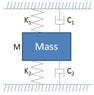
I have a mass-spring-damper system, as shown in the attahed picture, in which i have a mass suspended between two springs and dampers, each of which are attached to a fixed surface. he two opposite surfaces are part of the same fixed mass (i.e. the whole thing is inside a rigid box).


I know that a normal system with a single spring and damper can be expressed (in the Laplace domain) as

k / (k + Cs + ms^2)

But I can't work out how to modify the equation to include the mass and spring on the other side!

Any advice would be most welcome!

Thanks,

Andrew

 

[dynamicsolo]

I know that a normal system with a single spring and damper can be expressed (in the Laplace domain) as

k / (k + Cs + ms^2)

But I can't work out how to modify the equation to include the mass and spring on the other side!

You'll need to find the effective spring constant of the two springs and the effective damping constant of both dampers. Consider displacing the mass from equilibrium: how is the force from each spring directed? With the mass in motion, at a given moment, how is each damper resisting the velocity? The answers will suggest a way to combine the actions of the springs and of the dampers to represent the set with a single spring constant and damping constant.

 

[helium4amc]

Are they effectvely in series? If the mass is displaced, one of the springs tries to push it back into place, while the other one pulls it back into place? Equally, when the mass is in motion, both the dampers resist the motion equally?

Does that mean the expression becomes

[k1 + k2] = ([k1+k2s] + [C1+C2]s + ms^2)

Or am I being stupid?

 

[dynamicsolo]

Are they effectvely in series? If the mass is displaced, one of the springs tries to push it back into place, while the other one pulls it back into place? Equally, when the mass is in motion, both the dampers resist the motion equally?

Does that mean the expression becomes

[k1 + k2] = ([k1+k2s] + [C1+C2]s + ms^2)?

Well, the dampers apparently don't act equally, since the diagram suggests different damping constants, but they do act in concert. So, yes, I believe the proper treatment is simply to sum the spring constants and sum the damping constants. (Should that 's' be in the term on the right-hand side for the spring constants?)

BTW, although the springs look like they're in series, when one acts on either side of a mass, they actually behave like two springs side-by-side acting on one side of the mass, so they're properly speaking 'in parallel'. (Springs obey the same equivalent constant rules as capacitors and inductors do in electrical networks: for parallel components, individual constants add; for series components, reciprocals of the individual constants add to give the reciprocal of the equivalent constant.)

 

[helium4amc]

Excellent! Thank you very much for your help! And yes, I did mean [k1+k2].

Are the dampers comparable to Inductors and masses comparable to Resistors?

Thanks again,

Andrew

 

[noushin]

Hi dear andrwe
I have a project exactly same as yours.
I am pleased if you send for me the differential equation that you found.
you wrote [k1 + k2] = ([k1+k2s] + [C1+C2]s + ms^2)
but I've understood why [k1+k2s] and why there is s near k2
Any advice would be most welcome!
thank you noushin