Math Challenge by Erland #1

[Greg Bernhardt]

Submitted by @Erland
Solution Credit: @mfb

RULES:
1) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
2) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
3) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
4) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.

CHALLENGE:
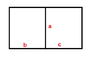
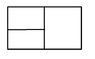
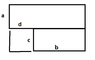
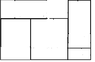
A rectangle is divided into a finite number of subrectangles. The sides of the subrectangles are all parallell to sides of the large rectangle.
Each subrectangle has at least one side with integer length.

Prove that the large rectangle also has at least one side with integer length.

 

[Comeback City]

LW is original rectangle. Divide it into a finite number of subrectangles (4 are shown, but any number could work), each with a length Z, which is an integer value. Therefore...
L = Z + Z + Z + Z
L = 4(Z)
Length of original rectangle must also be an integer value.

 

[mfb]

Length of original rectangle must also be an integer value.

If you divide it like that. You have to show that there is no possible division for non-integer values. You can't do that by picking a single one and showing that this specific one does not work.

The problem is not as easy as it might look.

 

[Comeback City]

If you divide it like that. You have to show that there is no possible division for non-integer values. You can't do that by picking a single one and showing that this specific one does not work.

The problem is not as easy as it might look.

Well I guess I'm going to take the L on this one then

 

[Erland]

The subrectangles might form a quite irregular pattern, like the attached one. All that is given is that each subrectangle has a side which has integer length. It could be the horizontal side, the vertical side, or both, and this might differ between the subrectangles.

 

[mfb]

I don't know if it leads to a proof, but if there is a solution, then there is also a solution where no two rectangles share exactly one side. This step is quite easy to prove.
Unfortunately there are patterns with more than one rectangle where no two rectangles share exactly one side.

 

[Buffu]

A subrectangle has the integer side parallel to length of large rectangle and another subrectangle has the integer side parallel to breadth of larger rectangle. Those subrectangles have only one integer side.

Is this possible ?

 

[mfb]

Sure.
Those two subrectangles don't cover the whole rectangle, however.

 

[Erland]

The only solution to this problem I know of is short, surprising, and beautiful, but almost impossible to find out if one doesn't already know it. Therefore, I'll give a hint:

Consider the complex valued integral $\int_a^b e^{2\pi i x}dx$, with $a$ and $b$ real. Under what conditions is this integral $0$?

If you think along these lines, you might find the solution.

It this hint doesn't help, I'll elaborate on it in a few days.

 

[mfb]

That is amazing.

Spoiler

Consider the integral $$\int_{x_{min}}^{x_{max}} dx \int_{y_{min}}^{y_{max}} dy e^{2 \pi i (x+y)} = \left(\int_{x_{min}}^{x_{max}} dx e^{2 \pi i x} \right) \left( \int_{y_{min}}^{y_{max}} dy e^{2 \pi i y} \right)$$
It is zero if and only if x_max-x_min or y_max-y_min is an integer. It is an integral of a function over a rectangle, therefore we can write it as sum of several integrals over subrectangles. For each subrectangle, the same rules apply: The integral is zero if one of the side lengths is an integer. All our subrectangles satisfy this condition, therefore the large rectangle has to satisfy it as well (0+0+...=0): at least one side length has to be an integer.

Edit: Generalized integration limits.

 

[Erland]

Very good mfb, but you must fix the integration limits. Even if the large rectangle has a vertex at the origin, the subrectangles will not.

Edit: mfb fixed this. The present solution is correct.

 

[mfb]

Well, sure, the integral is obviously invariant under a shift of lower and upper limit together. I generalized the integration limits.

 

[Comeback City]

Oh dang I wish I knew what all of that meant I need to reattempt teaching myself calculus now. @Erland what does that integral you gave out even represent?

 

[Erland]

Well, sure, the integral is obviously invariant under a shift of lower and upper limit together. I generalized the integration limits.

This is not true in general. For example: $\int_{-1/2}^0e^{2\pi i x} dx\neq \int_0^{1/2}e^{2\pi i x}dx$.
You obviously understand the idea, but this detail is unclear in your solution.

 

[Erland]

Oh dang I wish I knew what all of that meant I need to reattempt teaching myself calculus now. @Erland what does that integral you gave out even represent?

It does not represent anything in particular, it just can be used to prove the proposition.

 

[mfb]

This is not true in general. For example: $\int_{-1/2}^0e^{2\pi i x} dx\neq \int_0^{1/2}e^{2\pi i x}dx$.
You obviously understand the idea, but this detail is unclear in your solution.

... for the question if it is zero or not. After your first comment I changed my previous post to take the more general integration limits into account.

 

[Erland]

Now it is right! Very good! You'll have the credit mfb!

 

[QuantumQuest]

Just a simple observation regarding the given of the problem. We can make the assumption

Each subrectangle has at least one side with integer length.

as "each subrectangle has at least one pair of sides with integer length", as we're talking about rectangles. Now, we can work for a random such subrectangle using the hint by Erland, with the function $f(x,y) = e^{2\pi i x}e^{2\pi i y}$ and integrate it over its sides i.e $\int_a^b\int _c^d e^{2\pi i x}e^{2\pi i y}\,dx\,dy$. Now, if we calculate this integral, it turns out that it equals zero, if and only if at least one of the differences of its sides is an integer i.e. if b - a or d - c is an integer (I have done the calculation but I omit it here). But according to the above (modified) assumption each subrectangle has at least a such pair, so the integral of $f$ over it is zero. So, the integral over the whole rectangle is also zero. Then, this whole rectangle must also have an integer pair of sides and a fortiori one integer side. Just wondering if it is correct way to solve it.

 

[Erland]

Yes it's a correct solution, Quantum Quest. It is essentially the same solution as mfb's, but mfb came before you and gets the credit. Of course, for a rectangle, the conditions "at least one side has integer length" and "at least one pair of parallell sides have integer length" are equivalent.

 

[Comeback City]

but mfb came before you and gets the credit.

Did we already forget who came before mfb?

 

[ddddd28]

Oh dang I wish I knew what all of that meant I need to reattempt teaching myself calculus now. @Erland what does that integral you gave out even represent?

For those of us who are not familiar with complex integrals (still in high school...) I would like to present my own attemp. I can't assure my proof is 100% correct, but still, please, tell me what you think and how to improve it.
-----------------------------------------------------------------------------------
The intuition is to delete the subrectangles one by one according to some rules and leave bigger and bigger rectangles until only our external rectangle is left.
First lemma:
Given a rectangle which consists of two smaller rectangles, and they satisfy: "at least one side with integer length", thus, the big rectangle also satisfies this condition.
Proof:

a is an integer ⇒ the big rectangle has at least one side with an integer length.
a is not an integer⇒ b is integer and c is integer ⇒ b+c is an integer, the big rectangle has at least one side with integer length.
q.e.d
Second lemma:
Given a rectangle which consists of three smaller rectangles, as showed in the sketch, and they satisfy: "at least one side with integer length", thus, the big rectangle also satisfies this condition.

proof:
Use the first lemma twice.

Third lemma:

Elongate bd to h.

Let abcd cefg be rectangles with an integer side. (assume ab is the integer, if ac is the integer, it is really the same, just rotate the sketch)
Then, cghd and dhfe also have an integer side.
proof:

ab is an integer⇒ cd is an integer⇒cghd satisfies the lemma.
If ef is an integer ⇒ dhfe satisfies the lemma.
ef is not an integer⇒ ec is an integer ⇒ ec-dc is an integer ⇒ed is an integer⇒dhfe satisfies the lemma.
q.e.d.
According to the first lemma, we can draw:

--------------------------------------------------------------------------------------------------------------------

Let's examine Erland's sketch:
First, we should apply the first and the second lemmas to simplify the sketch.
We get:

Wow! it simplified very well! each of these rectangles has an integer side.
Here is where the third lemma comes to save us.
Let's apply it to the middle rectangle. (I will show the option where the horizontal lines are the integers, but it works also to the vertical lines.)

Now, it's piece of cake...
Just use the first and the second lemmas again, and you can prove that the original rectangle has an integer length.
I believe it should always work. If you disagree, please explain your position, and try to correct the proof.

 

[mfb]

Let abcd cefg be rectangles with an integer side. (assume ab is the integer, if ac is the integer, it is really the same, just rotate the sketch)

Let ac=1, ab=pi, cg=pi, gf=4. Splitting it into three rectangles fails, as you create a pi squared rectangle, no matter how you rotate it.

I was at that point as well.
There are other ways to rearrange rectangles, but you need a proof that you can simplify every possible pattern with these operations, and that is far from trivial.

 

[ddddd28]

Let abcd cefg be rectangles with an integer side. (assume ab is the integer, if ac is the integer, it is really the same, just rotate the sketch)
Then, cghd and dhfe also have an integer side.

Actually, what I meant is that we can't say which of the sides is an integer. But the proof is the same, and it is enough to show that it works for one side, since we can always find in the rectangle:

I hope it is more convincing.

 

[ddddd28]

I think I should have added this rule too: d is integer

 

[mfb]

Individually the posts work, but you cannot combine them. With the sides from my previous post:

 

[ddddd28]

Individually the posts work, but you cannot combine them. With the sides from my previous post:

View attachment 204648

I don't need to combine them...

 

[mfb]

Your approach was based on combining everything to get a contradiction. How does that work if you don't combine rectangles?

 

[ddddd28]

Your approach was based on combining everything to get a contradiction. How does that work if you don't combine rectangles?

"to get a contradiction"?
For the third lemma I had to make an assumption that the integer side is known. I claim that there is always an order of rectangles which satisfies the third lemma( both vertically and horizontally), and if not, there is the forth lemma. So far, I always succeeded to combine all the rectangles.
Give an example in which my rules are not enough.

 

[mfb]

"to get a contradiction"?

You don't necessarily have to write it like that, depends on the direction you take. Doesn't matter.

I claim that there is always an order of rectangles which satisfies the third lemma( both vertically and horizontally), and if not, there is the forth lemma.

Well, you claim that, but can you prove it? It doesn't work as you described in my example. It will work if I make a complete tiling out of it, but that is not the point.