Math Challenge - November 2018

[julian]

In principle yes, but I have difficulties to read your various quotients. Especially the nominators look wrong, as if you used $\frac{a+b}{c+d}=\frac{a}{c}+\frac{b}{d}$. He always crawls a constant distance on an increasing track. Just add the portions.

I was assuming the tree only grows during the daytime, and that the beetle only walks during the night. What should I be assuming?

 

[Keith_McClary]

7. How many times a day is it impossible to determine what time it is, if you have a clock with same length (identical looking) hour and minutes hands, supposing that we always know if it's morning or evening (i.e. we know whether it's am or pm).

Say the clock has circumference $1$ and $H$ and $M$ are the distances of the of the hands from the top. Clockwise. Then legitimate positions are
$$M=12H+r$$
where $-r$ is the integer part of $12H$. Ambiguous times satisfy this and also
$$H=12M+s$$
where $s$ is an integer.
Eliminating $M$ we find that $143H$ must be an integer. The ambiguous times occur at times $12n/143$ hours for $n=0, ..., 142$.

 

[fresh_42]

I was assuming the tree only grows during the daytime, and that the beetle only walks during the night. What should I be assuming?

Day by day is sufficient: units of 24 hours: +20 cm for the tree, +10/L for the beetle.

 

[Buzz Bloom]

There is no need to distinguish night and day. Steps of 24 hours are sufficient. And he needs more than 5 years.

Hi fresh:

Thanks for your post #90. I understand that I could have combined the two motions (beetle and tree) in the same row, but for the purpose of making clear the non-simultaneous movements of beetle and tree, I decided to use a separate row in the spreadsheet for each distinct movement. I also found my careless error of reversing the speeds of the tree and the beetle. I will be editing the post with this correction soon.

Regards,
Buzz

 

[fresh_42]

I will be editing the post with this correction soon.

Better make a new one. To be honest, it would help a lot if an answer "xyz days" was at the end. Then I could either look for an error or confirm it.

 

[Buzz Bloom]

Hi @fresh_42:

I corrected my spreadsheet, but my post #88 no longer permits me to edit it. Can you allow me to make edits in this post, or should I post my corrected solution in a new post?

Regards,
Buzz

BTW: My corrected answer is 3191 days = 8.736483 years (1 year = 365.25 days).
SPREADSHEET IMAGES

Spoiler

 

[fresh_42]

Hi @fresh_42:

I corrected my spreadsheet, but my post #88 no longer permits me to edit it. Can you allow me to make edits in this post, or should I post my corrected solution in a new post?

Regards,
Buzz

BTW: My corrected answer with is 3191 days = 8.736483 years (1 year = 365.25 days).
SPREADSHEET IMAGES

Spoiler

https://www.physicsforums.com/attachments/234518 https://www.physicsforums.com/attachments/234519 https://www.physicsforums.com/attachments/234520

Can you show us how you derived this result - in mathematics, not in excel?

 

[Buzz Bloom]

Can you show us how you derived this result - in mathematics, not in excel?

Hi fresh:
I have made some partial progress with the math, but before I complete what I have started I would appreciate your comments regarding the approach I am taking.

Spoiler

I put the relationships for b_n into an equation:

(b_n+1 - b_n) - U_n b_n = V_n,
U_n = 20/(t₀+20n), and
V_n = 20n.​

.
Unfortunately, I am unskilled in difference equations, but I let

x = n,
dx = 1 (day),
y(x) = b_n = beetle's position on day n,
u(x) = U_n = 1/(1+Ax),
A = T₀/20,
T₀ = 10000cm, and
v(x) = 10x = V_n = 10n.​

This gives me a differential equation

y'(x) - y(x)/(1+Ax) = 10x, A = T₀/20.​

I also let

t(x) = T_n = 20n + T₀ = height of tree on day n.
​

To find an approximate number of days, I need to solve the following equation for x.

y(x) = w(x).​

Would this approach give me an acceptable solution for problem #4?

Regards,
Buzz

 

[fresh_42]

Hi fresh:
I have made some partial progress with the math, but before I complete what I have started I would appreciate your comments regarding the approach I am taking.

Spoiler

I put the relationships for b_n into an equation:

b_n+1 - b_n U_n = V_n​

Unfortunately, I am unskilled in difference equations, but I let

x = n,
dx = 1 (day),
y(x) = b_n,
u(x) = U_n, and
v(x) = V_n.​

This gives me a differential equation

y'(x) - u(x) y(x) = v(x).​

I also let

w(x) = t_n.​

To find an approximate number of days, I need to solve the following equation for x.

y(x) = w(x).​

Would this approach give me an acceptable solution for problem #4?

Regards,
Buzz

You have a good result, i.e. within acceptable error margins, but I have no idea what you are talking about. What are $b,x,y,u,v,U,V$ and $w$? I only see a letter salad.

You started with $b_{n+1} - b_nU_n=V_n$. Fine but what do $b,U,V$ stand for?
From there you get $y'(x)-y(x)u(x)=v(x)$. How? You can write $y'(x)=b_{n+1}-b_n$ but I think you set $y'(x)=b_{n+1}$ and where lucky by the form of the equation that this only costed you a day.

This puzzle really doesn't need a lot of formulas, one single sum to be exact. To solve it via a differential equation looks fun but isn't necessary. But that's not the point. The point is that you did not define your letters and how you achieved your initial recursion!

 

[Buzz Bloom]

The point is that you did not define your letters and how you achieved your initial recursion!

H fresh:

I apologize for skimping on the details. I have edited my post #98, fixing typos and adding details. I hope it is now clear.

Regards,
Buzz

 

[fresh_42]

H fresh:

I apologize for skimping on the details. I have edited my post #98, fixing typos and adding details. I hope it is now clear.

Regards,
Buzz

I still find that you haven't explained a lot, especially what your letters should mean, except $b_n$ and $y(x)$ which have already been the easiest to guess. I still don't know what $u,v,w,U,V$ are. But as your solution is close enough and I can see the right formulas shine through, and I do not want to ride this horse to death, I accept this as an answer and add 'my solution':

On the first night the beetle manages $10/10000$ of the tree trunk. On the second night he crawls $10/10020$ of the tree trunk. On the third night he crawls $10/10040$ of the tree trunk. He has reached the top when the sum of the track parts reaches $1$.
\begin{align*}
\sum_{n=0}^{N}\dfrac{1}{1000+2n}&\geq 1\\
\sum_{n=0}^{N}\dfrac{1}{500+n}&\geq 2\\
\sum_{n=1}^{N}\dfrac{1}{n} - \sum_{n=1}^{499}\dfrac{1}{n}& \geq 2\\
H_N - H_{499} \geq 2
\end{align*}
The closest estimation is $H_n=\gamma +\log(n)+\varepsilon$ with the Euler-Mascheroni constant $\gamma$ and a small error $\varepsilon$, which yields $N=3688$ and $3688-499=3189$ nights. The least lower bound are $3184$ nights, which I got by nested intervals and wolframalpha.

Correction: A close estimation is $H_n=\gamma +\log(n)+\varepsilon$ with the Euler-Mascheroni constant $\gamma$ and a small error $\varepsilon$. A numerical solution yields at least $3691-499=3192$ nights. (cp. post #108 f.)

 

[Delta2]

for 10 d), do we have to find an example for which the limits of both sides exist and are finite (yet they differ)?
I think I have an example where left side limit is +infinite while right side limit is zero. Does this count?

 

[Keith_McClary]

4.
Ant on a rubber rope - Wikipedia

 

[fresh_42]

for 10 d), do we have to find an example for which the limits of both sides exist and are finite (yet they differ)?
I think I have an example where left side limit is +infinite while right side limit is zero. Does this count?

Yes. Lebesgue integrability and finite limits.

 

[Delta2]

Yes. Lebesgue integrability and finite limits.

Something else, I see the domain of the functions $f_r$ is $\mathbb{R^{+}}$ while the domain of the integral is $\mathbb{R}$.. Is this a typo? The domain of the integral should be also $\mathbb{R^{+}}$ right?

 

[fresh_42]

Something else, I see the domain of the functions $f_r$ is $\mathbb{R^{+}}$ while the domain of the integral is $\mathbb{R}$.. Is this a typo? The domain of the integral should be also $\mathbb{R^{+}}$ right?

Consider the $"+"$ as the typo. It isn't necessary. It should have been $r>0$. (corrected)

 

[Delta2]

ok here is my attempt at 10 d)

I consider $f_r(x)=|r|e^{-|r||x|}$

Then $$lim_{r\rightarrow 0}f_r(x)=0$$ so the right hand side of the condition is simply 0.

$$\int_{\mathbb{R}} f_r(x)dx=|r|\int_{\mathbb{R}}e^{-|r||x|}dx=|r|\frac{2}{|r|}=2$$ hence the left hand side is 2.

 

[Buzz Bloom]

Hi fresh:

I have just realized that I had misunderstood the quote below.

Can you show us how you derived this result - in mathematics, not in excel?

I had interpreted this as telling me that the spreadsheet approach was not acceptable, and that I needed to present a solution using mathematics. I now understand that what you were telling me was that I needed to include a mathematical explanation of what I was doing in the spreadsheet. I apologize for my denseness.

Here is my attempt to give a mathematical explanation of my spreadsheet images in my post #96, which I have edited to correct typos in the spreadsheet images.

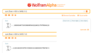
Column A
Whole numbers represent the number of the day of daytime growth of the tree starting at day 0 when the tree's height was 10000 cm.
Numbers with .5 represents the nighttime of the immediately preceding entry daytime, and corresponds to the nighttime in which the beetle climbs.

Column B
These values show the height of the tree on the day shown in Column A.
Also in the second image starting with cell B4 and continuing in all lower cells is the formula

=B(k)+20​

where k refers to the row of the cell two above the formula. This shows the calculation of the height of the tree by adding 20 cm to the previous day's height.

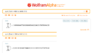
Column C
These values show the height on the tree to which the beetle has climbed on the day shown in Column A. The increases in the height value occur in both rows with and without the ".5" in Column A. In Column C with rows without ".5" in Column A, the increment in Column C calculates the increase in the beetles height due to the tree growth. The formula in cell C4,

=C3*B4/B3,​

shows that the previous beetle height is multiplied by the ratio of the previous tree height to the current tree height. In Column C with rows with ".5" in Column A, the increment in Column C calculated the increase in the beetles height due to the beetles climb that night. The formula in Cell C5,

=$C$3+C4,​

shows the beetle's height following the previous night's climb is added to the value in Cell C3 which is the constant 10cm of a nightly beetle climb.

Column D
These values (after Cell D1) show the ratio of the tree height (Column B) with the beetle's height (Column C). The formula in these cells show the calculation of these ratios. The bottom image shows the rows preceding and including the row in which the ratio value in Cell D6385 exceeds 1. The value in Cell A6385 shows that the beetle reached to top of the tree during its nightly climb on day 3191.

BTW: The quote below from your post #101.

The least lower bound are 3184 nights, which I got by nested intervals and wolframalpha.

gives the day the beetle reaches the tree top as 3184. I attempted to reproduce this in a spreadsheet calculating
ln(499) = 6.21260609575152
ln(3687) = 8.21256839823415
ln(3688) = 8.21283958467648
ln(3687)-ln(499) = 1.99996230248263
ln(3688)-ln(499) = 2.00023348892496
3688-499 = 3189

I then also calculated for the following sums for n=3190 and n=3191.
[NOTE: CORRECTIONS MADE TO NEXT TWO LINES.]
For n = 3190: $\sum_{i=0}^n 1/(500+k)$ = 1.99990946718039
For n = 3191:$\sum_{i=0}^n 1/(500+k)$ = 2.00018039646784

It appears that 3191 is more correct than either 3184 or 3189.

Regards,
Buzz

 

[fresh_42]

It appears that 3191 is more correct than 3189.

Wolframalpha says 3192 is correct. I don't know anymore how I got 3184. But if it takes eight years, who wants to fight about a week more or less; poor beetle.

I guess it depends on how exact a floating point processor works. I only know for sure that I will not check it manually.

 

[jim mcnamara]

For problem #4 which bugged me for bit - I've programmed too much not to try some C code - this version uses a 128 bit long double, my answer is 3198 (or 3197 if there is some tiny rounding error)
Probably a precision error, since my result varies from Wolfram Alpha, too.

// bug.c
#include "min.h"

void
iterate(long double limit)
{
   long double i=0.;
   long double sum=0.;
   int cnt=0;
   for(sum=0., i=500.; sum<limit; sum+=1./i)
   {
     cnt++;
     i+=1.;
   }
   printf("cnt iterations= %d\n", cnt);
}

int main(void)
{
   iterate(2.);
   return 0;
}

gcc -Wall -o bug bug.c
$ ./bug
cnt iterations= 3198

 

[Keith_McClary]

10 d)

$f_r(x)=|r|e^{-|r||x|}$

Other solutions:
$f_r(x) = 1/r$ on $[0,r]$ and $0$ elsewhere.
$f_r(x) = r$ on $[0,1/r]$ and $0$ elsewhere.

 

[Buzz Bloom]

Wolframalpha says 3192 is correct.

Hi fresh:

Apparently 3192 is more accurate with it's 39 decimal places of precision in its calculation, but I confess it surprises me that the accumulation of round-off errors of

0.00027092928745​

by my using only 14 decimal places would show up with only 3191 terms in my summation.

Regards,
Buzz

 

[Delta2]

Other solutions:
$f_r(x) = 1/r$ on $[0,r]$ and $0$ elsewhere.
$f_r(x) = r$ on $[0,1/r]$ and $0$ elsewhere.

These look good but
As for the 1st) the limit $\lim_{r\rightarrow 0}f_r(x)=\infty$ and @fresh_42 wanted finite limits in both sides.

As for the 2nd) if $r>0$, then $\int_{\mathbb{R}} f_r(x)dx=r\frac{1}{r}=1$
but if $r<0$ then $\int_{\mathbb{R}} f_r(x) dx=\int_{1/r}^0 r dx=r(0-1/r)=-1$ so the limit $r\rightarrow 0^{+}$ is $1$ while the limit $r\rightarrow 0^{-}$ is $-1$. I think this suggestion would work if we put $r$ and $1/r$ in the definition, under absolute value.

 

[fresh_42]

These look good but
As for the 1st) the limit $\lim_{r\rightarrow 0}f_r(x)=\infty$ and @fresh_42 wanted finite limits in both sides.

The limit at this single point might be infinite, but the integral is not, so both sides are defined. That's why I said Lebesgue integrability to shorten this discussion.

As for the 2nd) if $r>0$, then $\int_{\mathbb{R}} f_r(x)dx=r\frac{1}{r}=1$
but if $r<0$ then $\int_{\mathbb{R}} f_r(x) dx=\int_{1/r}^0 r dx=r(0-1/r)=-1$ so the limit $r\rightarrow 0^{+}$ is $1$ while the limit $r\rightarrow 0^{-}$ is $-1$. I think this suggestion would work if we put $r$ and $1/r$ in the definition, under absolute value.

That was the version before my correction. As you have pointed out, the $"+"$ had been misplaced as $r \in \mathbb{R}^+$ was meant. It makes not really a difference mathematically to consider all $r$ here, especially as it's easy to adjust.

My

Spoiler: example

$f_r(x) = \begin{cases} 0 & \text{if } |x| \geq r \\ \frac{r-|x|}{r^2} & \text{if } |x| < r \end{cases}$ we have $\int_\mathbb{R}f_r(x)\,dx=1$ for $r>0$ and $\lim_{r \to 0}f_r(x)=f_0(x)=\begin{cases}\infty &\text{ if } x=0\\ 0 &\text{ if }x \neq 0\end{cases}$ and so
$$
1 =\lim_{r \to 0}\int_\mathbb{R}f_r(x)\,dx\neq \int_\mathbb{R}\lim_{r\to 0}f_r(x) \,dx =0
$$

is basically the same, only that I used a triangle instead of a rectangle; and you used a bump, so all three are more or less the same.

 

[Delta2]

The limit at this single point might be infinite, but the integral is not, so both sides are defined. That's why I said Lebesgue integrability to shorten this discussion.

You are right, the integral exists and is zero, I just thought you meant no infinities at all when taking limits.

That was the version before my correction. As you have pointed out, the $"+"$ had been misplaced as $r \in \mathbb{R}^+$ was meant. It makes not really a difference mathematically to consider all $r$ here, especially as it's easy to adjust.

Ok now I noticed that $r>0$ , I didn't look carefully after you did the correction in the statement.

 

[Infrared]

It doesn't matter whether f_r(0) tends to \infty or not. You can consider the same family of functions but with f_r(0)=0 and nothing changes.

 

[Buzz Bloom]

In problems (12. a) and (12. b) the following notation appears in the integrals.

In (12. a): dλ(x) and dλ(y)
In (12. b): dλ(x,y)​

The dλ(x,y) notation does not appear in posts #62 and #70 in which @Keith_McClary solves problem (12. b).

What does the "λ" mean in these notations?

 

[fresh_42]

In problems (12. a) and (12. b) the following notation appears in the integrals.

In (12. a): dλ(x) and dλ(y)
In (12. b): dλ(x,y)​

The dλ(x,y) notation does not appear in posts #62 and #70 in which @Keith_McClary solves problem (12. b).

What does the "λ" mean in these notations?

$\lambda$ stands for the measure which is used for integration, normally Lebesgue. The only point here is, that I do not want to bother about any possible discontinuities of the function, as long as they are negligible, and Lebesgue integration gives me that, and in notation it is $\lambda$ = Lebesgue measure. This means we can integrate e.g. $\int_\mathbb{R}\chi_{(0,1)}(x)\,d\lambda(x)$ without having to deal with any limits at $x=0,1\,.$

And yes, @Keith_McClary could in general be a bit more detailed in his answers, especially for those of our many (silent) members who just read this thread and aren't necessarily familiar with the subject to an extend, at which those keywords are sufficient.

I'm not sure if I had posted it yet, as this thread became quite long in the meantime, so here goes the extended version of 12.b):

The function $f(x,y)=\dfrac{1}{x^2+y}$ is positive on $A=(0,1)\times (0,1)$ so we may apply the theorem of Fubini and get
$$
\int_0^1\int_0^1 \dfrac{1}{x^2+y}\,dy\,dx
=\int_0^1\left.\log (x^2+y)\right|_{y=0}^{y=1}\,dx = \int_0^1 [\log(x^2+1)-\log(x^2)]\,dx
$$
The logarithm function is monotone increasing and positive on $[1,2]$ so $\int_0^1\log(x^2+1)\,dx \leq \log 2\,.$ Furthermore we have
$$
\int_0^1\log(x^2)\,dx=2\cdot \left[x\log(x)- x \right]_0^1=-2
$$
and $\int_A \dfrac{1}{x^2+2}\,d\lambda(x,y) \leq 2 + \log 2 < \infty\,.$

 

[Keith_McClary]

apply the theorem of Fubini

I think it is a condition of Fubini that either the $x$ or $y$ integral be finite. (So you need to re-order your steps.)

 

[fresh_42]

I think it is a condition of Fubini that either the $x$ or $y$ integral be finite. (So you need to re-order your steps.)

Positive almost everywhere is sufficient.