Math of charts derrived from projectile motion equations

[ScientificMind]

Recently I was playing around with the idea of graphs of projectile motion and I started wondering what it would look like if someone were to graph every parabolic trajectory of a single initial velocity over all angles between o and 90 degrees above the horizontal. I decided to find out so in excel, I used the equation y=tanθ⋅x−x²⋅g/(2⋅v_i²⋅cos²θ), with an initial velocity of 6, a gravitational acceleration of 9.8, and 180 different angles, all between 0 and 90 degrees. The resulting chart this:

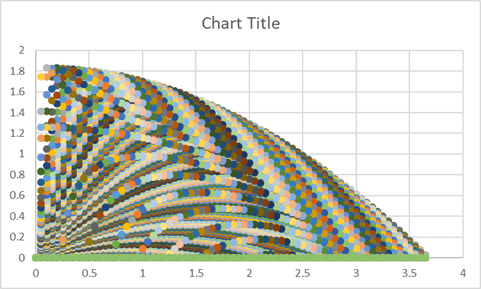
What I want to know is if it is possible to derive an equation for the curve above the area that this chart is approximating, partly out of curiosity about the equation itself and partly out of curiosity about whether it would be possible to then integrate that equation to find out the area of under that curve. I am also wondering if that shape has a name.

In addition, while playing around with this idea, I also made this chart:

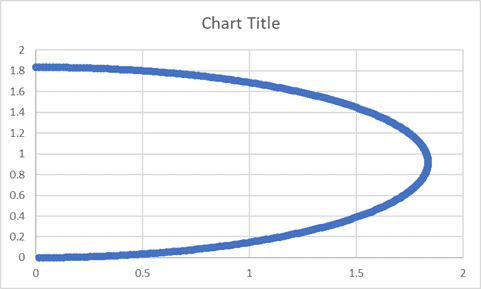
which graphs only the vertices of 360 versions of the above equation. Each vertex was obtained using x=(v_i²⋅sin(2θ))/(2⋅g) and y=(v_i²⋅sin²θ)/(2⋅g). Like with the other chart, I'm wondering if it is possible to derive an equation for the graph that this chart is approximating.

 

[mfb]

The envelope is a parabola on its own, example 5 at the Wikipedia page is the free fall you studied.

 

[ScientificMind]

The envelope is a parabola on its own, example 5 at the Wikipedia page is the free fall you studied.

Thanks a bunch! I didn’t know that was called an envelope before so it’s really nice to have a name for that kind of thing, and the Wikipedia page looks pretty interesting. Still, from what I can tell, it seems like the second chart, derived from only plotting the vertices of the various parabolas, wouldn’t count as an envelope. Do you know anything about that?

 

[ScientificMind]

Quick update: I decided to extend the chart that only graphs the vertices of the parabolas to include the vertices from equations using equations with angles between 0 and 180 degrees instead of just up to 90 degrees, and this is the result:

It looks like an ellipse. Does anyone know why it looks like an ellipse and whether it is an actual ellipse or not?

 

[mfb]

Each vertex was obtained using x=(v_i²⋅sin(2θ))/(2⋅g) and y=(v_i²⋅sin²θ)/(2⋅g).

Define $C=\frac{v_i^2}{2}$, then $x=C\sin(2\theta)$ and $y=C\sin^2(\theta)$.
Now calculate $x^2 + \left(y-\frac{C}{2}\right)^2$ and interpret the result.