Mathematica Mathematica: Generate Surface Equation

[mattmatt]

Hi there,
I just began using Mathematica today and I was wondering if there is a way to make the program generate an equation of a surface given a 3d array?

What I need it to do is to give me an equation of the surface so that given any two variables I can find the value of the third one.

Any advice will be highly appreciated.

Here is a screenshot of what the surface looks like:

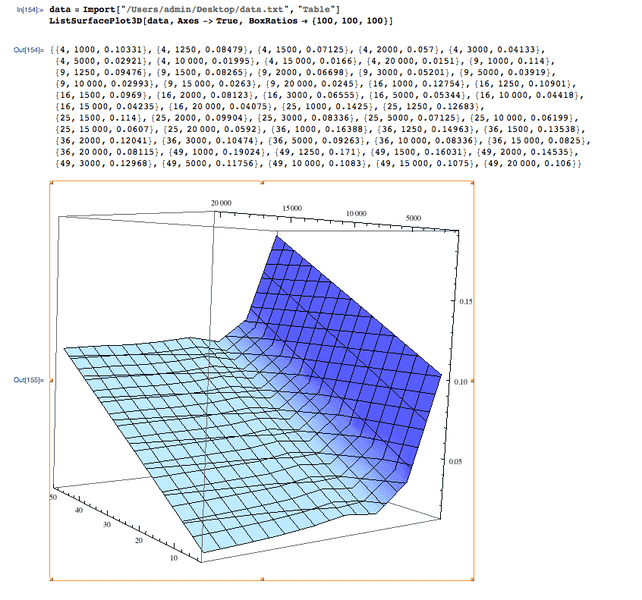
And here is the array:

4 1000 0.10331
4 1250 0.08479
4 1500 0.07125
4 2000 0.05700
4 3000 0.04133
4 5000 0.02921
4 10000 0.01995
4 15000 0.01660
4 20000 0.01510
9 1000 0.11400
9 1250 0.09476
9 1500 0.08265
9 2000 0.06698
9 3000 0.05201
9 5000 0.03919
9 10000 0.02993
9 15000 0.02630
9 20000 0.0245
16 1000 0.12754
16 1250 0.10901
16 1500 0.09690
16 2000 0.08123
16 3000 0.06555
16 5000 0.05344
16 10000 0.04418
16 15000 0.04235
16 20000 0.04075
25 1000 0.14250
25 1250 0.12683
25 1500 0.11400
25 2000 0.09904
25 3000 0.08336
25 5000 0.07125
25 10000 0.06199
25 15000 0.06070
25 20000 0.05920
36 1000 0.16388
36 1250 0.14963
36 1500 0.13538
36 2000 0.12041
36 3000 0.10474
36 5000 0.09263
36 10000 0.08336
36 15000 0.08250
36 20000 0.08115
49 1000 0.19024
49 1250 0.17100
49 1500 0.16031
49 2000 0.14535
49 3000 0.12968
49 5000 0.11756
49 10000 0.10830
49 15000 0.10750
49 20000 0.10600

 

[SteamKing]

That's generally a very hard problem, unless you already know the basic equation of the surface.
In those situations where the basic equation is known, you can use your surface data to fit the equation to the surface using regression techniques. Still a lot of number crunching though, and what if the equation doesn't pass through the surface data in one or more regions?

 

[Chronos]

Taming surfaces to keep them from extending beyond where they are intended to go is a black art. I used to model 3D surfaces on an IBM 360 in FORTRAN on punch cards. It was ... educational.

 

[mattmatt]

The equation doesn't have to be perfect, as long as it's a close approximation.
I found another program that can do this. It has a database of hundreds of basic equations and it fits the best one automatically for you. I was wondering if Mathematica can do this.

In the case of this example it spat out the following: