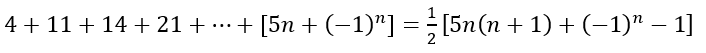Yankel
- 390
- 0
Dear all
I am trying to prove by induction the following:
View attachment 8712
I checked it for n=1, it is valid. Then I assume it is correct for some k, and wish to prove it for k+1, got stuck with the algebra. Can you kindly assist ?
Thank you.
I am trying to prove by induction the following:
View attachment 8712
I checked it for n=1, it is valid. Then I assume it is correct for some k, and wish to prove it for k+1, got stuck with the algebra. Can you kindly assist ?
Thank you.