Happiness
- 686
- 30
Why isn't the second line in (5.185) ##\sum_k\sum_l<\phi_m\,|\,A\,|\,\psi_k><\psi_k\,|\,\psi_l><\psi_l\,|\,\phi_n>##?

My steps are as follows:
##<\phi_m\,|\,A\,|\,\phi_n>##
##=\int\phi_m^*(r)\,A\,\phi_n(r)\,dr##
##=\int\phi_m^*(r)\,A\,\int\delta(r-r')\phi_n(r')\,dr'dr##
By the closure relation (5.63a) below,
##=\int\phi_m^*(r)\,A\big(\int\sum_l\psi_l(r)\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
##=\int\phi_m^*(r)\,A\big(\sum_l\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
Since ##A## is a linear operator,
##=\int\phi_m^*(r)\sum_lA\big(\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr\big]##
Since ##A## acts on ##r## and not ##r'##,
##=\sum_l\big(\int\phi_m^*(r)\,A\,\psi_l(r)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big)##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\int\delta(r-r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
By the closure relation (5.63a) below,
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\int\sum_k\psi_k(r)\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\sum_k\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
Since ##A## is a linear operator,
##=\sum_l\big[\int\phi_m^*(r)\sum_kA\big(\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
##=\sum_k\sum_l\big[\int\phi_m^*(r)\,A\big(\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
Since ##A## acts on ##r## and not ##r''##,
##=\sum_k\sum_l\big(\int\phi_m^*(r)\,A\,\psi_k(r)\,dr\,\,\times\,\,\int\psi_k^*(r'')\psi_l(r'')\,dr''\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big)##
##=\sum_k\sum_l<\phi_m\,|\,A\,|\,\psi_k><\psi_k\,|\,\psi_l><\psi_l\,|\,\phi_n>##
Derivation of the closure relation (5.63a):
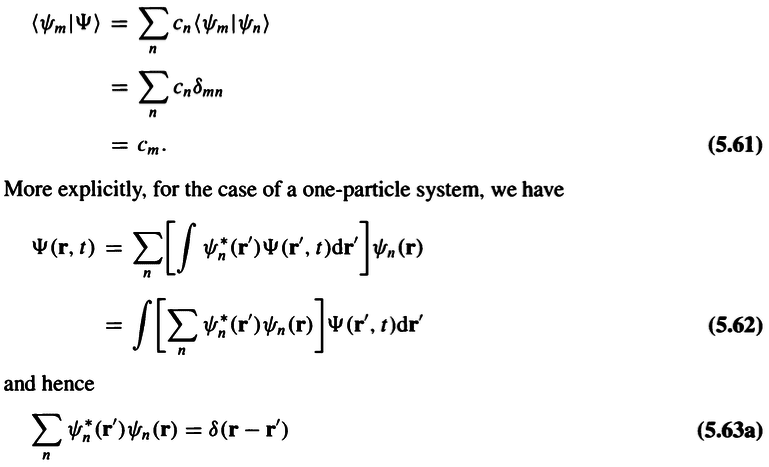
My steps are as follows:
##<\phi_m\,|\,A\,|\,\phi_n>##
##=\int\phi_m^*(r)\,A\,\phi_n(r)\,dr##
##=\int\phi_m^*(r)\,A\,\int\delta(r-r')\phi_n(r')\,dr'dr##
By the closure relation (5.63a) below,
##=\int\phi_m^*(r)\,A\big(\int\sum_l\psi_l(r)\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
##=\int\phi_m^*(r)\,A\big(\sum_l\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
Since ##A## is a linear operator,
##=\int\phi_m^*(r)\sum_lA\big(\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\psi_l(r)\int\psi_l^*(r')\phi_n(r')\,dr'\big)dr\big]##
Since ##A## acts on ##r## and not ##r'##,
##=\sum_l\big(\int\phi_m^*(r)\,A\,\psi_l(r)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big)##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\int\delta(r-r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
By the closure relation (5.63a) below,
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\int\sum_k\psi_k(r)\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
##=\sum_l\big[\int\phi_m^*(r)\,A\big(\sum_k\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
Since ##A## is a linear operator,
##=\sum_l\big[\int\phi_m^*(r)\sum_kA\big(\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
##=\sum_k\sum_l\big[\int\phi_m^*(r)\,A\big(\psi_k(r)\int\psi_k^*(r'')\psi_l(r'')dr''\big)dr\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big]##
Since ##A## acts on ##r## and not ##r''##,
##=\sum_k\sum_l\big(\int\phi_m^*(r)\,A\,\psi_k(r)\,dr\,\,\times\,\,\int\psi_k^*(r'')\psi_l(r'')\,dr''\,\,\times\,\,\int\psi_l^*(r')\phi_n(r')\,dr'\big)##
##=\sum_k\sum_l<\phi_m\,|\,A\,|\,\psi_k><\psi_k\,|\,\psi_l><\psi_l\,|\,\phi_n>##
Derivation of the closure relation (5.63a):
Last edited: