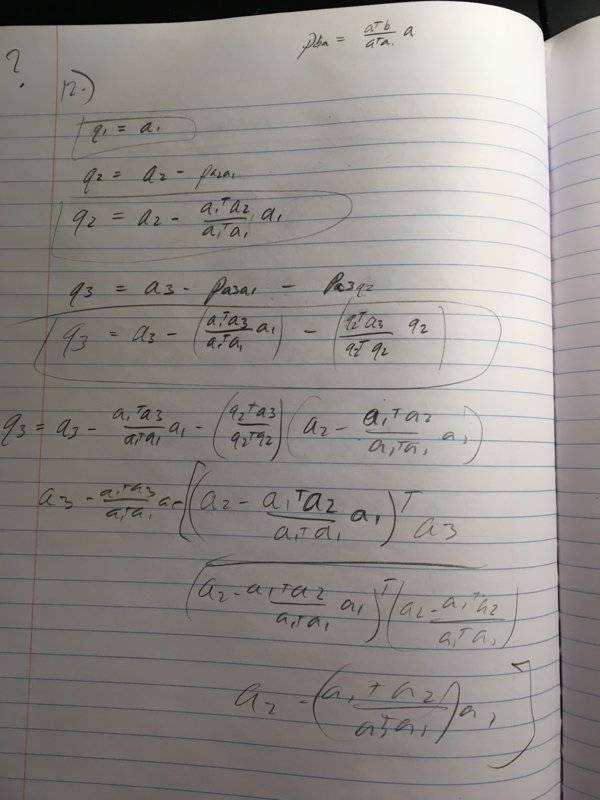Matrix which reverses Gram-Schmidt - Linear Algebra

[Amadeo]

Homework Statement

Let a1, a2, a3 be linearly independent vectors in R 3 , and let q1, q2, q3 be the vectors obtained from a1, a2, a3 by the Gram-Schmidt algorithm.

Define the linear transformation T : R 3 → R 3 by T(q1) = a1, T(q2) = a2 and T(q3) = a3.

For the choice of basis {q1, q2, q3} both for the input and output spaces, find the matrix MT which represents the linear transformation T for this choice of basis.

Relevant Equations

projection equation used in Gram-Schmidt: p=((a^t)(b))/((a^t)(a)) (a)

My idea was to write out the formulas for the orthogonal q vectors in terms of the input vectors using the basics of gram-schmidt. Then, I would rewrite those equations suhc that the a vectors were written in terms of the q vectors. And then, try to find some matrix which would capture the needed transformation. However, the q vectors must be written in terms of multiple a vectors, as well as other q vectors. Additionally, the need to make all of the orthogonal vecotrs of unit length makes it even more complicated. There must be another way.

 

[Addez123]

If a1-3 are linearly independent vectors, shouldn't q1 = a1, q2 = a2, q3 = a3?

Because Gram-Schmidt method is about substracting the part of your vector that's represented in previous vectors. But there are no such parts since they are linearly independent.