- 1,200
- 711
Attachments
-
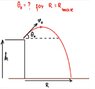 Maximum-Range-diagram-1.jpg6.8 KB · Views: 317
Maximum-Range-diagram-1.jpg6.8 KB · Views: 317 -
 Maximum-Range-diagram-1.jpg6.7 KB · Views: 229
Maximum-Range-diagram-1.jpg6.7 KB · Views: 229 -
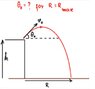 Maximum-Range-diagram-1.jpg6.8 KB · Views: 258
Maximum-Range-diagram-1.jpg6.8 KB · Views: 258 -
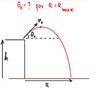 Maximum-Range-diagram-1.jpg6.8 KB · Views: 224
Maximum-Range-diagram-1.jpg6.8 KB · Views: 224 -
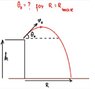 Maximum-Range-diagram-1.jpg6.7 KB · Views: 241
Maximum-Range-diagram-1.jpg6.7 KB · Views: 241 -
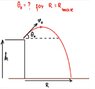 Maximum-Range-diagram-1.jpg6.8 KB · Views: 207
Maximum-Range-diagram-1.jpg6.8 KB · Views: 207 -
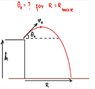 Maximum-Range-diagram-1.jpg6.8 KB · Views: 219
Maximum-Range-diagram-1.jpg6.8 KB · Views: 219 -
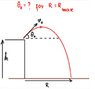 Maximum-Range-diagram-1.jpg6.8 KB · Views: 200
Maximum-Range-diagram-1.jpg6.8 KB · Views: 200 -
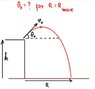 Maximum-Range-diagram-1.jpg6.7 KB · Views: 219
Maximum-Range-diagram-1.jpg6.7 KB · Views: 219 -
 Maximum-Range-diagram-1.jpg6.8 KB · Views: 192
Maximum-Range-diagram-1.jpg6.8 KB · Views: 192 -
 Maximum-Range-diagram-1.jpg6.8 KB · Views: 329
Maximum-Range-diagram-1.jpg6.8 KB · Views: 329 -
 Maximum-Range-diagram-1.jpg5.1 KB · Views: 457
Maximum-Range-diagram-1.jpg5.1 KB · Views: 457
Last edited by a moderator: