ItsukaKitto
- 10
- 4
- Homework Statement
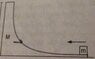
- A body of mass M with a small block of mass m placed on it, rests on a smooth horizontal plane. The surface of the body M is horizontal near the smaller mass and gradually curves to become vertical. The block is set in motion in the horizontal direction with a velocity v. To what height, relative to the initial level, will the block rise after breaking off the body M? Friction is assumed to be absent.
- Relevant Equations
- F = ma, momentum conservation
Conservation of energy
Total work = ∆K.E.
Diagram attached at the endI personally think there's something wrong with this question, and I'd like if someone can tell me whether it's the question that is wrong or my approach.
If I attempt the solution thinking that M should be stationary, the solution is simple. 0 - 1/2 mv^2 = -mgh, gives h = v^2/(2g). However, this is not the right answer, so I assumed the lower block moves (because this problem was given in a section titled "momentum" ), but for mass M to move, there should be a force on it...which can only arise if there is friction.
If I assume friction is present, I get the velocity
w = mv/(M+m) as the common velocity for m and M.
And to obtain the height, I can use the work energy theorem:
>>> W(gravity) + W(friction) = 1/2 m(v1)^2 + 1/2Mw^2 - 1/2mv^2
note: here v1 is the velocity of the block as it breaks off with M.
I found that W(friction) = -v^2(Mm)/2(M+m)
So substituting and setting v1 = w, (as I think, the horizontal component when the block is breaking off, wouldn't change) I get:
>>>2*W(gravity) = w^2(m + M) - mv^2 + v^2(Mm)/(M+m)
>>>-2mgh = v^2(m^2)/(m+M) - mv^2 + v^2 (Mm)/(M+m)
>>> Meaning that h is precisely zero...(is it?)
When I checked the answer to this problem, it was actually Mv^2/2g(m+M) and I found out a way they could have arrived at this:
Using conservation of energy, and ignoring the work done by friction:
1/2 mv^2 = 1/2 m(v1)^2 + 1/2 Mw^2 + mgh
Now setting v1 = w, we get:
mv^2 - (m+M) w^2 = 2mgh
>> h = Mv^2 /2g(M+m)
I don't think this approach is right, because if they are considering friction, why are they ignoring the work it does?
If I attempt the solution thinking that M should be stationary, the solution is simple. 0 - 1/2 mv^2 = -mgh, gives h = v^2/(2g). However, this is not the right answer, so I assumed the lower block moves (because this problem was given in a section titled "momentum" ), but for mass M to move, there should be a force on it...which can only arise if there is friction.
If I assume friction is present, I get the velocity
w = mv/(M+m) as the common velocity for m and M.
And to obtain the height, I can use the work energy theorem:
>>> W(gravity) + W(friction) = 1/2 m(v1)^2 + 1/2Mw^2 - 1/2mv^2
note: here v1 is the velocity of the block as it breaks off with M.
I found that W(friction) = -v^2(Mm)/2(M+m)
So substituting and setting v1 = w, (as I think, the horizontal component when the block is breaking off, wouldn't change) I get:
>>>2*W(gravity) = w^2(m + M) - mv^2 + v^2(Mm)/(M+m)
>>>-2mgh = v^2(m^2)/(m+M) - mv^2 + v^2 (Mm)/(M+m)
>>> Meaning that h is precisely zero...(is it?)
When I checked the answer to this problem, it was actually Mv^2/2g(m+M) and I found out a way they could have arrived at this:
Using conservation of energy, and ignoring the work done by friction:
1/2 mv^2 = 1/2 m(v1)^2 + 1/2 Mw^2 + mgh
Now setting v1 = w, we get:
mv^2 - (m+M) w^2 = 2mgh
>> h = Mv^2 /2g(M+m)
I don't think this approach is right, because if they are considering friction, why are they ignoring the work it does?