Maximum Induced Voltage of an AC Generator

[LePainguin]

I would like to ask a question about the induced voltage of an AC generator. So, according to a graph I found on Google, the maximum induced voltage is reached when the loop is parallel to the loop. (The graph shown below.)

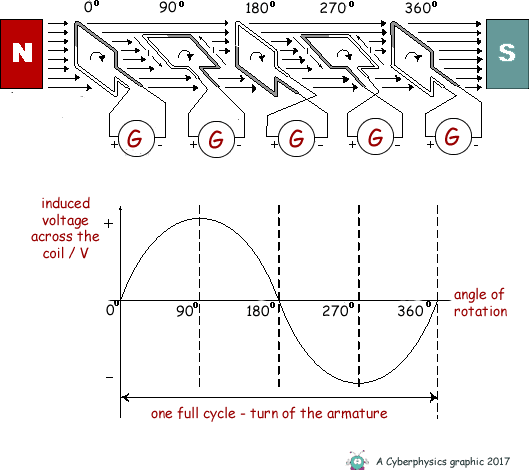
Then I was wondering, what if the loop is initially (when it is at 0 degrees) parallel to the magnetic field instead of it being perpendicular like in the graph. Would it reach the maximum induced voltage when the loop is perpendicular now, or would it still be when it's parallel?

 

Then I was wondering, what if the loop is initially (when it is at 0 degrees) parallel to the magnetic field instead of it being perpendicular like in the graph. Would it reach the maximum induced voltage when the loop is perpendicular now, or would it still be when it's parallel?

Why would it? All you're doing is a relabelling of coordinates $\theta'= \theta -\pi/2$, and you still should expect the same physical results - that the greatest induced EMF occurs when the loop is horizontal.

 

[Delta2]

This is due to a property of the $\sin (\omega t+\phi)$ function regarding its first and second derivative.

Indeed the flux through the loop is $$\Phi=A_0\sin\theta(t)$$ where $\theta(t)=\omega t +\phi$ the angle the loop makes with the field at time t.
The induced voltage is then $$\mathcal{E}=-\frac{d\Phi}{dt}=-\omega A_0\cos\theta(t)$$
The maximum or minimum of the voltage is when $$\frac{d\mathcal{E}}{dt}=0\Rightarrow\omega^2 A_0 \sin\theta(t)=0\Rightarrow \theta(t)=k\pi, k=0,1,2,...$$

So the maximum or minimum is when the angle the loop makes with the field is $k\pi$ which in other words means when the loop is parallel with the field. And this result is independent of the initial angle $\phi=\theta(0)$ that the loop makes with the field at t=0.

PS: My angle $\theta(t)$ is defined as the angle the tangential to the loop makes with the field lines. Your schematic seems to define the angle $\theta'(t)$ as the angle of the normal to the loop makes with the field lines. Hence the two angles relate by the equation $$\theta'(t)=\theta(t)+\frac{\pi}{2}$$.