- #1
foo9008
- 678
- 4
Homework Statement
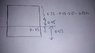
A platform is supported by a rectangular plastic tank below . When there's no external load act on it , it oscillate on the water surface with amplitude 0.05m . When it's in equilibrium , the water reaches 0.07m of the height of tank submerged in water.
P/s : the tank has a height of 0.35m , and base area of 0.5 (m^2) . Assume it is undamped oscillation
what is the maximum load it can withstand so that the platform still can float on water ?
Homework Equations
The Attempt at a Solution
when it's in equlibrium , the tank submerged 0.06m , the amplitude of oscillaltion is 0.05m , so 0.35m - 0.06m -0.05m = 0.24m ? so the maximum load = buoyant force = (0.24)(1000)(9.81) N , am i right ? The weight of platfrom is then subtracted from (0.24)(1000)(9.81) N to get the max load it can withstand...
is my working correct ?
Attachments
Last edited: