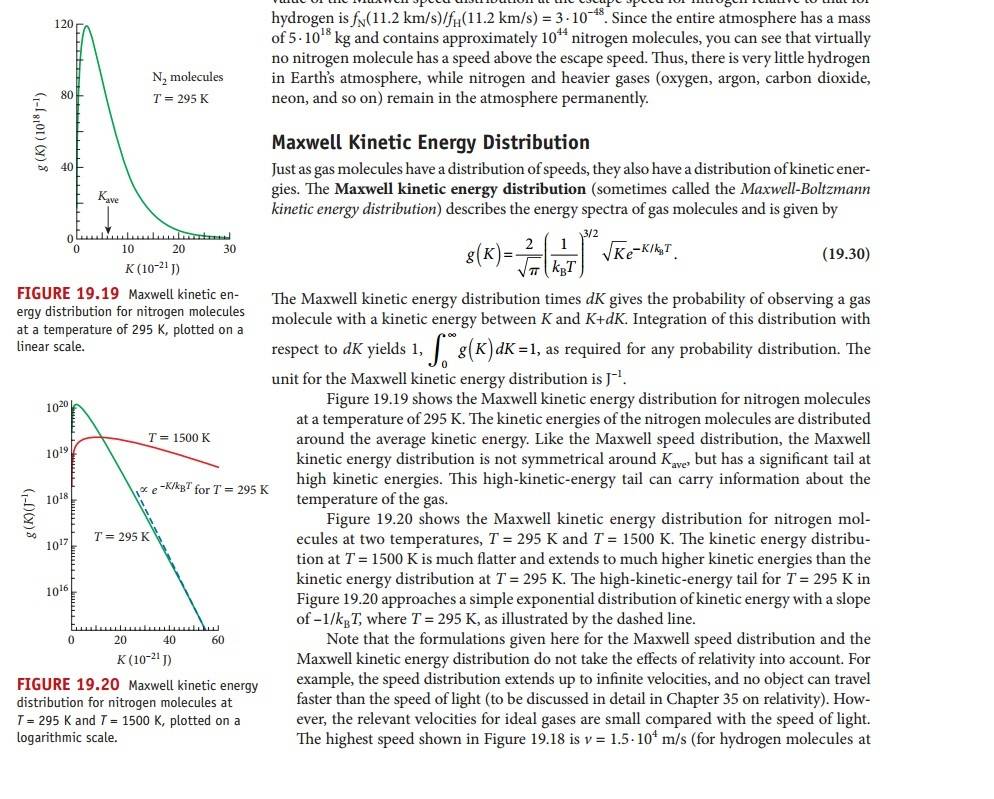
Discussion Overview
The discussion revolves around calculating the kinetic energy distribution of nitrogen molecules using the Maxwell Kinetic Energy Distribution (M.K.E.D). Participants explore the relationship between kinetic energy, temperature, and the distribution of molecular speeds, while seeking clarification on integration techniques and the interpretation of various formulas.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses uncertainty about starting the calculation of kinetic energy distribution and questions the interpretation of the kinetic energy formula.
- Another participant clarifies that K represents the kinetic energy of a molecule and suggests using molar kinetic energy or total kinetic energy depending on the context.
- A participant inquires about calculating the kinetic energy of a molecule within a specific range, K to K+dK.
- There is a distinction made between using K = 1/2*mv² and the mean kinetic energy formula 3/2kBT, with some arguing that K is simply a value rather than a function of gas properties.
- Multiple participants discuss the probability distribution function g(K) and its relation to the average kinetic energy of gas molecules at temperature T.
- One participant emphasizes the need for clarity on the specific problem being solved, suggesting that the integration of g(K) may be the goal.
- Another participant points out that the distribution of speeds differs from the distribution of energies and mentions the gamma distribution form of g(K).
- There are discussions about the limits of integration for calculating fractions of molecules with kinetic energy between two values, K1 and K2.
- Some participants suggest using Excel or other tools for numerical integration, while others seek a solution without calculators, referencing the gamma function and error function.
- One participant provides a detailed mathematical formulation involving the Maxwell distribution and suggests checking the anti-derivative for accuracy.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the specific problem being solved, with some focusing on integration techniques while others emphasize the interpretation of kinetic energy values. The discussion remains unresolved regarding the best approach to calculate the desired fractions of molecules.
Contextual Notes
There are limitations regarding the clarity of the problem being addressed, as well as the dependence on definitions and the need for numerical values in integration. The discussion also highlights the complexity of transitioning between different forms of energy distribution.