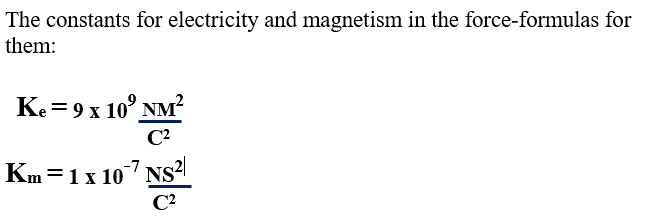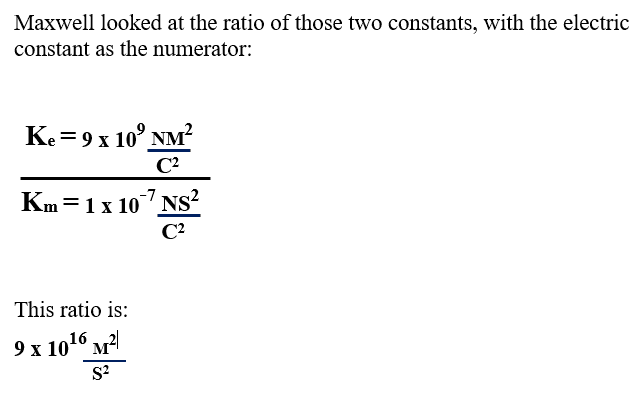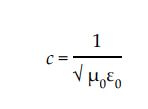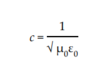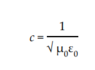I don't know, whether the question has been answered. There are two questions in one, namely about the mathematics of how to derive this result (that's quite easy to answer with sufficient math) and the historical one. The latter is very interesting but involved. The point is that electromagnetic waves have not been discovered yet. They were a prediction of Maxwell's theory. What was known of course was the speed of light, but it was not known that light in fact is a electromagnetic wave (at a frequency/wavelength the receptors in our eyes are sensitive to).
Here's the math. We start from Maxwell's equation for free electromagnetic fields, i.e., for a space-time region were no charges and currents are present, using SI units (spoiling of course the beauty of Maxwell's original equations)
$$\vec{\nabla} \times \vec{E}+\partial_t \vec{B}=0, \quad \vec{\nabla} \cdot \vec{B}=0, \quad \vec{\nabla} \times \vec{B} -\mu_0 \epsilon_0 \partial_t \vec{E}=0, \quad \vec{\nabla} \cdot \vec{E}=0.$$
The trick is to get rid of ##\vec{B}## from the 1st equation (Faraday's Law of Induction) by taking its curl:
$$\vec{\nabla} \times (\vec{\nabla} \times \vec{E}) + \partial_t \vec{\nabla} \times \vec{B}=0.$$
Now the "double curl" simplifies with the last equation to
$$\vec{\nabla} \times (\vec{\nabla} \times \vec{E})=\vec{\nabla} (\vec{\nabla} \cdot \vec{E}) - \Delta \vec{E} = -\Delta \vec{E}$$
while according to the 3rd equation (the Ampere-Maxwell Law)
$$\partial_t \vec{\nabla} \times \vec{B}=\mu_0 \epsilon_0 \partial_t^2 \vec{E}.$$
This indeed gives a wave equation for the electric field components alone,
$$(\mu_0 \epsilon_0 \partial_t^2 - \Delta)\vec{E}=0.$$
The phase velocity of the waves, ##c##, thus obviously fulfills
$$\frac{1}{c^2} = \mu_0 \epsilon_0.$$
Now, ##\mu_0## and ##\epsilon_0## can be thought of being measured with help of static (sic!) sintuations, given the unit of electric charge and currents, and that's indeed how historically the numerical values were found. Of course, it was in terms of the more natural electrostatic and magnetostatic systems of units, but the principle is the same as within the SI units, and indeed what you find when plugging in the values of the permeability and permittivity of the vacuum (which are despite their fancy names just arbitrary conversion factors to define the SI unit of electric currents, Ampere), is that ##c## agrees very well with the measured speed of light in a vacuum, and that's why Maxwell came to the conclusion that light is just an example for these waves.
Historically the experiment by Weber and Kohlrausch was crucial for the prediction of em. waves:
https://www.ifi.unicamp.br/~assis/Weber-Kohlrausch(2003).pdfhttps://aapt.scitation.org/doi/10.1119/1.1934570
It took over 30 years to directly prove him right: In 1888 Heinrich Hertz was the first to produce and detect electromagnetic waves in the physics lecture hall at Karlsruhe university. He was allowed to do these experiments only in the semester breaks not to disturb the lectures during the semester ;-))).