Dirkpitt
- 2
- 0
first off I'd like say thanks to everyone on here, I've lurked and solved many questions thanks to you guys. First post woo.
Basically we were tasked to design and carryout a lab to measure the coefficients of friction between a wooden board and some random objects (teachers gone for a few days so busy work basically). Easy stuff really, but I'm getting all confused with the components and way to solve for the coefficients/distinguish difference between solving for kinetic and static (if there is one).
Have a bunch of angles but only need some help on getting started.
Object 1 - Static 18 degrees to start moving, kinetic 13.6 degrees to move at a constant velocity.
This is where I'm lost basically.
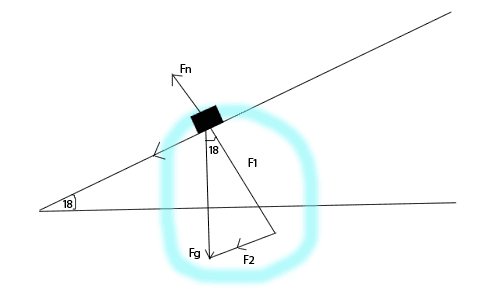
This is the diagram I have. Excuse my 5 minute pentool job XD. With similar triangles the angle is 18 degrees, and I know you have to use cos and sin to make up for the "F1, F2" variables. Cos for F1, and Sin for F2, all I'm missing is how to use them. Thus I haven't gotten too far yet :(
From my current understanding, Fn = Fg - Ff. So Normal force has to equal the force of gravity minus the force of friction for the object to move, I'm just not sure on how to add in the F1 and F2. I'm thinking F=mg would work, and setting them equal to each other?
Something like;
F1=M(Gcos)
F2=M(Gsin)
Then M(Gcos)=M(Gsin), you could take out the "M", since M=M.
Gcos=Gsin
G=Sin/Cos
G=Tan
Honestly I don't really know where I was going with that, other then taking out the M :/
Basically we were tasked to design and carryout a lab to measure the coefficients of friction between a wooden board and some random objects (teachers gone for a few days so busy work basically). Easy stuff really, but I'm getting all confused with the components and way to solve for the coefficients/distinguish difference between solving for kinetic and static (if there is one).
Homework Statement
Have a bunch of angles but only need some help on getting started.
Object 1 - Static 18 degrees to start moving, kinetic 13.6 degrees to move at a constant velocity.
Homework Equations
This is where I'm lost basically.
The Attempt at a Solution
This is the diagram I have. Excuse my 5 minute pentool job XD. With similar triangles the angle is 18 degrees, and I know you have to use cos and sin to make up for the "F1, F2" variables. Cos for F1, and Sin for F2, all I'm missing is how to use them. Thus I haven't gotten too far yet :(
From my current understanding, Fn = Fg - Ff. So Normal force has to equal the force of gravity minus the force of friction for the object to move, I'm just not sure on how to add in the F1 and F2. I'm thinking F=mg would work, and setting them equal to each other?
Something like;
F1=M(Gcos)
F2=M(Gsin)
Then M(Gcos)=M(Gsin), you could take out the "M", since M=M.
Gcos=Gsin
G=Sin/Cos
G=Tan
Honestly I don't really know where I was going with that, other then taking out the M :/