nate_cal
- 1
- 0
- TL;DR
- I do not really understand how to determine the value Q from the shear formula for this example.
Hello!
I am new to mechanics of materials and I am very confused about the problem below. So the shear formula is:
tau = VQ/It
From the book (Hibbeler) I understand that Q is "y'A', where A' is the cross-sectional area of the segment that is connected to the beam at the juncture where the shear flow is calculated, and y' is the distance from the neutral axis to the centroid of A'". However, for this case I do not understand why A' is only one of the top boards (red area) and not both, if the bolt goes through all the 3 boards.
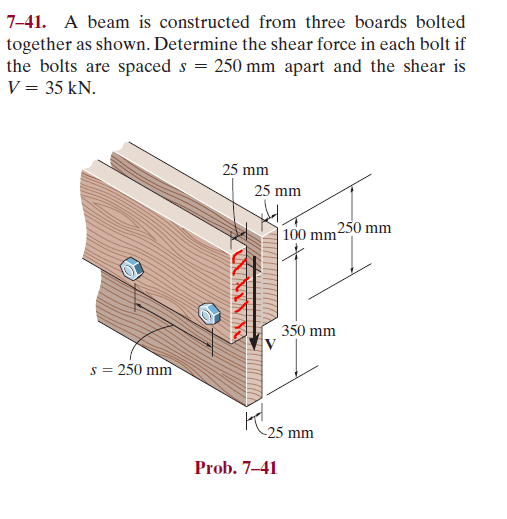
I am new to mechanics of materials and I am very confused about the problem below. So the shear formula is:
tau = VQ/It
From the book (Hibbeler) I understand that Q is "y'A', where A' is the cross-sectional area of the segment that is connected to the beam at the juncture where the shear flow is calculated, and y' is the distance from the neutral axis to the centroid of A'". However, for this case I do not understand why A' is only one of the top boards (red area) and not both, if the bolt goes through all the 3 boards.