Oblivion77
- 113
- 0
Mechanics:Dynamics (Newton's 2nd Law?)
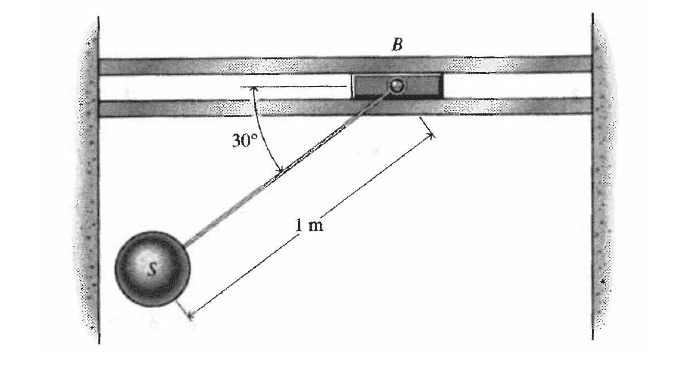
A sphere S with a mass of 5 kg is attached by a rigid rod to 1 kg block B which is free to slide with no friction in a horizontal slot. The system is released from rest. At the instant when it is released, find the tension in the rod and the accelerations of both blocks.
Sum of the forces in x = ma
Sum of the forces in y = ma
I am not exactly sure how to tackle this problem. Would I need to solve this using Newton's 2nd law? Or would this question require conservation of energy?
Homework Statement
A sphere S with a mass of 5 kg is attached by a rigid rod to 1 kg block B which is free to slide with no friction in a horizontal slot. The system is released from rest. At the instant when it is released, find the tension in the rod and the accelerations of both blocks.
Homework Equations
Sum of the forces in x = ma
Sum of the forces in y = ma
The Attempt at a Solution
I am not exactly sure how to tackle this problem. Would I need to solve this using Newton's 2nd law? Or would this question require conservation of energy?